Другие статьи

---

С.Л. Василенко, П.Я. Сергиенко

Математика и гармония целостности

К 1-му Международному конгрессу по математическим проблемам гармонии (Одесса, 2010)

"Математика есть поэзия гармонии, вычислившая себя, но не умеющая высказаться в образах для души"

Г. Лейбниц

Вступление. Актуальность проблемы научного подхода к гармонизации отношений современной цивилизации в системе координат "природа–цивилизация–человек" в нынешних условиях обусловлена ростом отношений дисгармонии жизненно важных сфер бытия, вплоть до души или духовности человека.

Разлад в этих областях в конечном итоге грозит существованию самой цивилизации.

Не будет преувеличением сказать, что энергетические мощности техносферы достигли потенциала природных стихий, а человеческий фактор в формировании отношений в ноосферной гармонии стал играть ведущую роль.

Разумеется, анализ этих отношений должен базироваться на строго выверенных научных началах.

Любое теоретическое исследование той или иной реальности мира выстраивается с использованием целенаправленной методологии и логического аппарата вполне определенных философских и математических методов. Известно, например, что в философии метод метафизики отличается от противоречивого ему метода диалектики, а в математике методы геометрии отличаются от методов алгебры. Выводы исследователей на базе данных методов так же часто разнятся. Не случайно в философии и математике прижились, так называемые, методы "непротиворечивости": в философии – триалектика; в математике – алгебраическая геометрия, дифференциальная геометрия и др.

Общепринято считать, что в реальном мире всё существует и проявляется гармонично (слаженно, согласованно) в своих противоположностях.

Данный принцип бытия присущ и самой гармонии в широком смысле этого слова.

В истории познания случилось так, что этому принципу, его проявлению и применению, особенно в математике, со стороны философов и математиков уделялось недостаточное внимание.

Этот пробел был частично восполнен исследователями только в конце ХХ века.

И как часто бывало в истории при разрешении тех или иных проблем, не обошлось без крайностей, в том числе, и в познании гармонии в её проявлениях через математику.

Одним из знаковых событий в этой связи стало озвучивание точки зрения редакции Академии Тринитаризма (она изложена в предисловии к статье [1]):

«Объективно математика гармонии (МГ) ещё отнюдь не сформирована до такого уровня, чтобы принять канонические "учебниковые" формы. У неё имеются два качественно разных уровня дальнейшей разработки, которые необходимо чётко и систематически различать».

Попытаемся и мы непредвзято разобраться в уровнях разработки МГ, разведя сущностные понятия категорий гармонии и математики по разные стороны баррикад, чтобы потом опять их свести вместе, но уже в одно унисонно-слаженное звучание.

Сразу признаемся, нам глубоко импонирует объединение смысловых конструкций, за которыми стоят математика и гармония. Идеологи, разработчики и последователи этого направления почувствовали тонкие вибрации находящей новой волны в познании мира.

Пожалуй, именно гармония способна стать объединяющим началом третьего тысячелетия в истории человечества. С математикой разговор особый.

Одновременно накладываются и определенные граничные условия, устанавливающие высокую планку ответственности за адекватное отражение вызовов времени.

Но все равно это посильная задача с ясной жизнеутверждающей целью.

Тревожит иное: легковесность, когда, не успев по настоящему оформиться, МГ уже претендует на роль спасителя для формализованного описании бытия, чему особо вредят отдельные дифирамбы-песнопения хвалебных од. Хотя речь идет пока лишь о робких попытках сформировать основы учения о гармонии систем.

Мы не собираемся персонифицировать данный лингвистический объект.

Мы также ни в коей мере не ставим под сомнение результаты конкретных исследований, которые вольно или невольно уже попали под вывеску МГ или вышли под ее логотипом. Речь идет исключительно о смыслах, значениях, предмете, объекте и прочих качественных атрибутах, которые могут описывать и представлять возможные инварианты словесного образа МГ с явной философской окраской, что пока слабо корреспондируется как с отдельно взятой математикой, так и с обособленной гармонией.

Данной статьей преследуется цель дать краткое изложение для читателей и оппонентов сути различия разных мировоззренческих и методологических начал к применению исследования гармонии целостности и математических начал ее моделирования.

В определенной мере это взаимосвязано с тематикой намечающегося 1-го Международного конгресса «Современные аспекты математики гармонии, и её применение в экономике, естествознании, технологии, социуме и образовании». В его подготовительных документах изложена главная цель, состоящая в развитии МГ и информировании участников о ее сути как нового междисциплинарного направления современной науки.

Мы надеемся, что участники конгресса обратят внимание на наше видение и осмысление поднимаемых проблем и учтут их при подготовке итоговых документов.

Исходные рубежи. В статье [2], посвященной геометрическим образам и закономерностям гармонии, высказаны некоторые соображения по поводу лингвистической и научной обоснованности словосочетания "МГ".

Данный вопрос представляется многоплановым и в определенной мере дискуссионным, но в любом случае требует развернутого представления, поскольку он может в целом стать основой для корректировки или смены парадигмы в естествознании.

Здесь важно с самого начала корректно очертить поле и правильно расставить вешки, чтобы не уйти в дебри или не заблудиться в трех соснах.

Поэтому за отправные положения примем точку зрения, что «различия вполне могут существовать, но только на основе общих убеждений … как базис коммуникации и понимания» [3]. И чтобы разуметь друг друга, сначала нужно принять некие общие представления о мироздании независимо от того, правильные ли они у каждого из нас в отдельности или нет. Иначе в процессе взаимного общения мы будем невольно искажать понимание слов оппонента и заранее считать, что он явно ошибается, не находя почвы для взаимопонимания.

Такой основой вполне может служить, прежде всего, общее осмысление и признание того, что существует два неких, пока будем говорить отдельных мира (области, сферы): мир гармонии реальной действительности и мир математики, как идеальной действительности.

Во всяком случае, многовековое развитие человеческой мысли дает основание так утверждать.

И здесь не очень важно сразу же пытаться выяснять до конца подлинный (истинный) смысл этих двух разных, а может быть, и не очень разных миров.

Важно принять за основу факт (в крайнем случае, рабочую гипотезу) их наличия, и ограничиться некими базовым набором общих характеристик, приемлемых для дальнейшего взаимного общения. Оно и понятно, ведь ни математику, ни гармонию мы сегодня не сможем облечь в некие униформы, дав им всеобъемлющие универсальные дефиниции. Хотя на обывательском уровне все выглядит донельзя просто.

Следующий этап – это поиск сфер возможно взаимного соприкосновения и пересечения мира математики и мира гармонии. Это чрезвычайно важный момент в философском и методологическом аспектах. Он позволяет выйти на общее понимание вопроса: на предмет их сопоставления, соотнесения, дополнения и т.п.

Именно здесь могут рождаться самые разные словесно-смысловые сложноподчиненные конструкции, как-то "гармония математики", "гармоничная математика", "математика в гармонии", "математические начала (основы, основания) гармонии" и т.д.

Но именно здесь, дабы не засорять "научный эфир" терминологией сомнительного толка, необходимо формирование и принятие приемлемых правил селекции, когда «принимаемые в качестве истинных предложения – лингвистическое представление убеждений – детерминируют значения входящих в них слов» [3], а согласованное восприятие картины мира создает общий и понятный язык коммуникаций.

Уместными становятся слова: «Сегодня зарождающаяся наука о гармонии напоминает лоскутное одеяло, где специалисты из разных областей "пришивают" каждый свой кусок. Это не критика, ибо понятно, что даже такое разношерстное "одеяло" – достижение современной мысли. Но далее – уродливость положения будет сказываться все более» [4].

Философско-методологические основания гармонии и математических начал целостности. Известно, что философия на протяжении тысячелетий изучала и объясняла сущность гармонии двумя методами: метафизическим и диалектическим.

Метафизика утверждает, что наш мир действительности не противоречив, вечен и неизменен.

Такому миру присуща предустановленная гармония равновесия и симметрии во всем.

Согласно материалистической диалектике мир действительности постоянно изменяется и развивается благодаря наличию противоречия между противоположностями всех явлений без исключения.

Таким образом, возникшие в древности два метода философствования являются также противоречивыми. Истина, как говорится, находится посредине.

Выражаясь телеграфным стилем, диалектическая (особенно материалистическая) философия проблему сущности гармонии обошла стороной, поскольку требовалось, в согласии с ее же методом, признать и метафизический взгляд на мир действительности.

Например, в философских словарях ХХ века практически отсутствует даже понятие такой категории или принципа как "гармония".

Не будет абсурдной мысль и о том, что белые пятна общефилософских методов, так или иначе, трансформировались на математические методы исследования.

В конце второго тысячелетия, в период "застоя" диалектического метода, в философии начал формироваться "триалектический" метод познания действительности. Причину его появления мы уже указали.

Гносеологические корни этого метода произрастают от тезиса древнегреческого философа Парменида[1] (6 в. до н. э): «Мысль и то, о чем она существует, есть одно и то же».

В историю философии этот тезис вошел как тезис «тождества бытия и мышления». Дискуссия вокруг сущностного содержания данного тезиса продолжается до наших дней. Инициирует ее фундаментальная теза материалистической философии: в мире нет ничего кроме движущейся материи в пространстве и времени. Согласно с этим положением утверждается, что бытие всего существующего – это материя, а мысль есть продукт материи (материя – первична, сознание – вторично).

Тезис триалектического метода философии – в мире нет ничего кроме движущегося триединого пространства.

Бытие движущегося пространства – это то, что можно мыслить в качестве всех видов реальности: материальной и идеальной, объективной и субъективной, физической, социальной и виртуальной.

Теоретически триединое пространство – это относительное пространство, рожденное взаимодействием абсолютных противоположностей пространства (пространства материи и пустоты, или в физическом понимании – пространства вещества и пространства вакуума).

Таким образом, триединое пространство исследуется, как некая единосущная, гармонично саморазвивающаяся целостность бытия, существующая в трех единовременных ипостасях.

В данном утверждении триалектики тезис философии материализма присутствует уже как частный случай более общей философии целостного восприятия мира. Заметим, «… все частные формы философствования, ведущие к утрате целостного восприятия мира, постепенно изживают себя, исчерпывая все свои возможности.

Объективно возникает потребность в обретении способности философии выразить духовную, культурную и политическую целостность, которая и в истории, и в настоящем начинается с триединства [5, с. 6–7].

Не обошло это стороной и такую категорию как "гармония".

Гармония. Разные попытки осмысления и количественного исчисления гармонии содержат:

– ранние идеи пифагорейцев о выражении пространственного соотношения космических сфер посредством числовых соотношений музыкальной октавы;

– более поздние искусы "проверить алгеброй гармонию" /A.С. Пушкин об Сальери/, математическое исчисление перспективы в живописи, эталонирование скульптур и др.

Мы не будем глубоко исследовать данную понятийную сущность, скажем, начиная с Пифагора. Это тема отдельного исследования. Но некоторые соображения стоит все-таки озвучить и проанализировать.

Гармония обычно связывается с соразмерностью, соответствием целого и частей.

Так она воспринимается и в эстетике, и в художественных объектах.

Сопоставимость целого и частей, а потом уже ощущение красоты – главный вопрос гармонии во многих предметных областях.

Такой же позиции придерживался и русский философ А.Лосев, чье определение приводится в Большой советской энциклопедии [6, с. 128]: «Гармония – соразмерность частей и целого, слияние различных компонентов объекта в единое органическое целое. В гармонии получают внешнее проявление внутренняя упорядоченность и мера бытия».

В переводе с греческого языка гармония принимает разные оттенки, такие как связь, порядок и строй, лад и слаженность, соразмерность и стройность, и вообще взаимное соответствие чего-либо.

В энциклопедическом словаре (http://www.edudic.ru/bes/13294) лосевский смысл гармонии (греч. harmonia, связь – стройность, соразмерность) дополняется ее древнегреческим философским пониманием как организованность космоса, – в противоположность хаосу.

Хотя, на наш взгляд, гармония не полна без своей условной половинки в виде организованного беспорядка или детерминированного хаоса.

В философии гармония – это установка или базовая ценность культуры (!), которая ориентируется на осмысление мироздания и человека с позиций их внутренней (глубинной) упорядоченности [7]. В измерениях аксиологии[2] она конституируется уже не столько в качестве скалярной (поддержание), сколько в качестве векторной (достижение) аксиологической структуры.

Гармония в философии [8] – это и состояние многого как единого целого, характеризующее слаженность членов сложных совокупностей, ансамблей, коллективов, участников единого действия в некотором данном фиксированном отношении. Гармония – есть приведенные к одному и тому же единству различия, противоречия или ограниченное до некоего узлового значения разнообразие в структурной организации объекта: внутренне непротиворечивое в гармонизации не нуждается.

Любопытно представление гармонии [9] через её характерные признаки:

– согласованность, связанность, единство всех элементов гармоничной системы;

– единство и борьба противоположных начал, контрасты;

– мера, пропорциональность и равновесие;

– ясность, легкость восприятия;

– уместность, соответствие, природосообразность;

– прекрасное, возвышенное;

– совершенство.

Словарь Даля[3] определяет гармонию как соответствие и созвучие, соразмерность, равновесие, взаимность, соотношение и согласие, стройность; соразмерное (правильное) отношение частей целого.

А вот Гегель смещает акценты с количества на качество[4]: "Гармония представляет собой соотношение качественных различий, взятых в их совокупности и вытекающих из сущности самой вещи".

Не ограничиваясь только соразмерностью, боле широкое определение дает В. Татур [10]: «Гармония – принцип соразмерности частей системы. Гармония не просто принцип соразмерности частей в целом, это – способ существования трансфинитного, бесконечного в финитном, конечном».

Существуют и многие другие частные определения гармонии, как правило, в областях музыки, живописи, архитектуры, социологии, политики и т.д.

Что же общего и не противоречивого в основных определениях? – Этимология слова.

Они указывают на то, что гармония есть некая внутренняя упорядоченность присущая целому. Большинство из них указывают на то, что гармонии присущ атрибут меры.

Только «Новейший философский словарь» определяет гармонию как установку культуры и мировоззренческую категорию бытия.

Именно в этом, на наш взгляд, ценность и жизненный смысл познания мер гармонии в многообразных областях человеческого бытия.

И если, как нам кажется, в данном определении слово "полагание" заменить словом "мера", тогда мы получим довольно приемлемое определение:

Гармония – установка культуры, ориентирующая на осмысления мироздания

(как в целом, так и его фрагментов) и человека

 с позиции меры и их глубинной внутренней упорядоченности.

В дополнение к сказанному можно особо выделить такой атрибут гармонии как симметрия или неизменность при каких-либо преобразованиях.

Симметрия, в частности, связывается с представлениями о гармонии и эстетическом совершенстве форм, начиная с эстетики Древней Греции.

Гармония как субстанциальная категория. Недостатком многих цитируемых выше определений гармонии является то, что они базируются только на атрибутах присущих самой гармонии, а не на субстанциальном принципе бытия, как то: принципе сохранения и принципе развития.

Понимание целого и части (частей) в триалектике базируется на древних европейских и восточных учениях о едином.

В соответствии с триалектическим принципом всеобщей связи в космической иерархии систем, входящих одна в другую, это означает:

· в мире нет такого целого, которое не являлось бы в том же смысле одновременно частью другого целого;

· всякая часть всегда одновременно обладает свойствами целого и в качестве такового познается.

Единому бытию, как целостному процессу движущегося пространства (субстанции), присущи два противоположных принципа:

– принцип изменения (развития) субстанции;

– принцип сохранения субстанции.

Эти два воззрения порождают третий принцип:

• принцип гармонии изменения и сохранения целого, где его частями являются данные субстанциальные принципы.

Принцип гармонии, таким образом, является объединяющей и управляющей субстанцией в целом. Он проявляется как следствие количественных отношений мер целого и его, противоположностей.

Кем, где и когда был философски сформулирован количественный принцип гармонии: «Большая часть целого так относится к его меньшей части, как целое относится к его большей части», доселе неизвестно.

Но правомерность его утверждения проверяли (решали, доказывали) методами математики (арифметики, геометрии или алгебры) уже в глубокой древности.

Количественно это отношение равно числовой константе 1,618... При этом следует отметить, что противоположная ей числовая константа отношения (меньшая часть целого так относится к его большей части, как большая часть относится к целому) равна 0,618…

И только, при алгебраическом ее выводе, символ "минус" перед ней свидетельствует о ее противоположности другой константе. Это аналогично тому, что число 0,636… (отношение диаметра к длине окружности в мерах радиуса) является константой, противоположной числу π ≈ 3,14159… Данные числа при изменениях структурной, фрактальной и масштабной гармонии остаются неизменными.

Дуализм гармонии и дисгармоничности. «В европейской философии понятие гармонии выступает в качестве категориального выражения сущностной внутренней связи внешне альтернативных начал» [7].

«Гармония складывается не иначе, как общий контур обнимает отдельные члены» (Леонардо да Винчи).

Но если в классической европейской культуре нормой служила исключительно гармония, то для модернизма в качестве нормы она мыслится уже дуальной, с ее оборотной стороной в виде дисгармоничности.

Следуя Гегелю (см. выше), мы даже усилили бы изложенные им позиции, связанные с соразмерностью, за счет ее замены на соотносительность или просто отношение, когда уже соразмерность соподчиняется и становится частным случаем.

Тогда совокупность обусловленных и взаимосвязанных причинно-следственных связей сама по себе, без всяких соразмерностей, – это тоже гармония.

Взаимное отношение пространства и времени – гармония. Ведь о какой соразмерности можно говорить, рассматривая пространство и время, как самостоятельные категории?

Гармония – отношение противоположных частностей в общности.

Это отношение общего вида, когда могут отсутствовать какие-либо характеристики соразмерности, либо они вообще отсутствуют в явном виде, как в топологии.

Сюда же можно отнести, например, частные суждения в общности интересов, культурные срезы общества, традиции и обычаи, социальную энергетику и др. с вполне приемлемым общим брендом: «Ничего лишнего и всё на месте» [11].

Гармония – широкое понятие. Она ближе к методологии, чем к отдельной науке.

Как ни странно, но система, раздираемая изнутри противоречиями, но сравнительно "мирно живущая" во внешнем окружении, – тем не менее, гармонична.

Возможно, она не так устойчива, но это уже другая категория и область исследования – сфера изучения границ и/или параметров ее устойчивости.

Гармония является таким же неотъемлемым атрибутом природы, как масса или энергия.

Солнце, в исчадие ада которого ежесекундно сгорают миллионы тонн вещества, с позиции земного наблюдателя выглядит просто прекрасно и гармонично.

Атомный взрыв также гармоничен, как и водопад, поскольку – он суть единства и одновременного проявления нескольких физических законов, объединенных совокупностью действий и последствий в одно целое.

Вулканы, без которых вряд ли стала возможной жизнь на Земле, – разве это не гармония? Или такие с виду не совсем гармоничные явления как катастрофы, являющиеся способом обновления, гибель галактик, возникновение новых звезд, сжигающих все вокруг себя, – это тоже величайшая гармония мироздания.

А вот очаровательная с виду бабочка, несмотря на свою истинную красоту, в определенном смысле вовсе негармонична, так как является только частью (малой толикой) единого жизненного цикла и метаморфозы четырех стадий превращения: «яйцо – личинка (гусеница) – куколка – имаго».

Метафора «Все в мире относительно» в наибольшей степени подходит как раз к принципу гармонии.

Если бы мир полностью отвечал неким стандартным параметрам, он был бы однообразен и скучен.

И если вспоминать золотое сечение (ЗС), то мир ЗС – не менее угнетающая картина, как и мир без ЗС.

С человеком вообще получается кривое зеркало. Наиболее заинтересованное в гармонии лицо, он сам – безудержный и потенциальный её нарушитель.

Любое познание начинается первоначально в его сознании с экспериментального выделения части познаваемого. Так мы расчленяем пространство и время, вещественную плоть и ее отсутствие (пустоту). Одновременно и невольно нарушаем и гармонию как связь нераздельных противоположностей целого.

В широком смысле гармония – по сути, есть мироздание, а вернее целостная совокупность его элементов (явлений, процессов), состояний и отношений.

С позиций наблюдателя это «ощущение функциональной и структурной оптимальности системы и ненарушающей взаимосвязи с другими окружающими системами» [11].

А вот любая математика, даже МГ, в ее прикладном значении – это все же анализ и разложение на части. Для синтетического видения проблемы полное погружение в чистую математику вредно. В интерпретации гармонии надо наоборот чаще подниматься над математикой, пытаясь увязать с известными знаниями о других сторонах бытия.

Гармония нередко присутствует и в науке, создавая лаконичные построения.

Но ее роль при этом невелика.

Она никогда не выступает критерием истины, и служит в основном для эстетического удовольствия ученых. Она никогда не принимается как серьезный или решающий аргумент за или против какой-нибудь теории или конструкции. Критерии научной истины другие.

Хотя если теория еще и образно красива, то она только от этого выигрывает.

Перезагрузка темы. Ниже мы еще вернемся к взаимообусловленным и взаимосвязанным понятиям математики и гармонии.

Пока только отметим, что в ряде своих определений под математикой понимается только наука о количественных соотношениях и их закономерностях, то есть как чисто абстрактная область знаний или чистая математика.

Именно тем, что математика «абстрактная наука, занимающаяся умственными построениями» [12, с. 529], она и выделяется особо среди других наук.

Основным атрибутом сущности чистой математики является число.

В литературе приводится много его определений как меры.

Наиболее обобщающее определение сводится к тому, что число – это абстракция, используемая для количественной характеристики объектов.

В чистой математике, в процессах комбинаторики чисел и символов проявляются некоторые абстрактные закономерности, которые имеют место, особенно в статических явлениях пространственной действительности.

Но, всегда ли, занимаясь символьными комбинациями чисел, например, чисел треугольной матрицы Паскаля, и, выявляя в ней всевозможные числовые закономерности, мы можем знать о том, какой реальной действительности они присущи?

Можем ли мы ведать какая пространственная форма закономерных отношений (числовых констант реальности) отражается той или иной матричной формой (линейной, треугольной, квадратной, прямоугольной, пятиугольной и т.д.) расположения одних и тех же чисел? – Мы в состоянии только вычислять количественные закономерности в основном арифметическими и алгебраическими методами при условии единой изначальной меры исчисления.

Пространственное представление об изначальной мере исчисления нам дает геометрия. Она является связующим математическим посредником между формой и количественным содержанием (числом) пространственной реальности. Принятыми в геометрии средствами, можно построить любое число, как меру пространства, и как меру отношения чисел.

В отличие от чистой математики геометрия дает человеку образное представление о пространственных формах и количественных реалиях действительности.

Именно геометрия является первой ступенькой в математическом познании действительности и формировании у человека о ней образного мировоззрения.

Чистая математика – это такой предмет, где мы не знаем, о чем мы говорим, и не знаем, истинно ли то, о чем мы говорим (Бертран Рассел).

Собственно такой нам представляется и канва учебника "Математика гармонии и современная наука» под ред. А. Стахова, проект которого он вынашивал довольно давно и кое в чем сомневался. В этой связи процитируем некоторые его высказывания [13]:

«Я выбрал название "Математика Гармонии" (может быть, не совсем удачное)... моя "Математика Гармонии" не претендует на роль "Всеобщей теории Гармонии"…

Подобно "теории Шеннона" моя "Математика Гармонии" описывает некоторый количественный аспект понятия "гармония", который основан на трактовке гармонии как связи и комбинации… И в этой науке важную роль будут играть числа Фибоначчи, золотое сечение и их обобщения, р-числа Фибоначчи и золотые р-сечения…

Я увидел, что введенное мною понятие "золотого р-прямоугольника", который при р = 0 совпадает с "двойным квадратом", при р = бесконечности – с традиционным квадратом, а при р = 1 – с классическим "золотым прямоугольником", может быть использовано в сакральной геометрии».

Прошло 7 лет после публикации этих и других похожих пояснений.

К результатам своих исследований автор, к сожалению, ничего нового так и не добавил.

Правда от собственных колебаний и сомнений со временем избавился, но первые и последующие критические замечания отбросил. А параллельное направление исследований в области математических начал гармонии геометрическим методом признал только спустя 7 лет, хотя его содержание и результаты в издаваемый учебник не включил.

Непредвзятый анализ дает основание утверждать, что основная, если не вся энергия его писательской и организационной деятельности в эти годы была направлена в основном на закрепление мирового приоритета своего направления исследований и его результатов.

Насколько это гармонично судить не беремся. – Об этом позаботится время.

А мы плавно перейдем к интересному феномену: роли, месте и значении гармонии в математике, прежде всего, глазами самих математиков, начиная с приведенного эпиграфа.

Гармония в математике. В согласии с диалектикой и триалектикой, пространство математического бытия является субстанцией идеальной реальности.

Определений математики, как предмета науки, существует много. Одно из первых классически обобщающих определений математики сделал Рене Декарт (1596–1650) французский математик, философ, физик и физиолог, создатель аналитической геометрии и современной алгебраической символики:

«К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики» [14].

"В сухом остатке", математика (греч. mathematike – от mathema наука) – наука о количественных отношениях и пространственных формах действительного мира <путем идеализации необходимых для этого свойств объектов и формализации этих задач>.

В более пространном описании это цикл наук, изучающих величины и пространственные образования (арифметика, алгебра, геометрия, тригонометрия и т.д.), включая чистую математику (занимается величинами отвлеченно), прикладную математику (прилагает ее к делу) и т.д.

Мы не будем цитировать другие определения математики, имеющие место быть. Скажем только, что абсолютно непротиворечивого понимания древнейшей науки, математики, не существует до настоящего времени.

Вместе с тем, подчеркнем, в традиционных определениях указывается, что математика – наука о количественных и пространственных отношениях реального (действительного) мира, а не идеального (символьного).

Все, что можно выразить цифрою, принадлежит математике, а ее изначально главное назначение – показать (отразить) гармонию мироздания и его отдельных частей.

Многие крупные ученые делились своими соображениями о математике.

Они искрометны фантазией. В них содержится аллегория.

Порой они окутаны поэзией гармонии с попыткой высказаться в образах для души.

Этим они ценны и позволяют по новому посмотреть на всю математику, ловя себя иногда на слове: а может это есть гармония или ее выжимка без дистиллированной воды?

 Судите сами...

«Математика – это наука, брошенная человечеством на исследование мира в его возможных вариантах» (И. Кант).

«Законы математики, имеющие какое-либо отношение к реальному миру, ненадежны; а надежные математические законы не имеют отношения к реальному миру» (А. Эйнштейн).

«Математика – царица наук» (К. Гаусс).

«Каждая математическая система … свертывает в себе огромные цепи и последовательности рассуждений, или мыслительных процессов, делая ненужными повторения их в дальнейшем при решении других задач» [15, лекция 4].

«Законы математики не относятся к той или иной области явлений природы, как законы других специальных наук, а ко всем и всяким явлениям, лишь взятым со стороны их величины; она по-своему универсальна, как тектология» [16, гл. 2, § 2].

Математика суха и одновременно поэтична.

Математические идеи могут вызывать эмоции, сравнимые с эмоциями, возникающими при чтении литературных произведений, слушании музыки, созерцании архитектуры.

Вот что писал выдающийся русский математик Н.Лузин (1883–1950): «Математики изумляются гармонии чисел и геометрических форм. Они приходят в трепет, когда новое открытие открывает им неожиданные перспективы. ... Математик изучает свою науку вовсе не потому, что она полезна. Он изучает ее потому, что она прекрасна. <...> Я говорю о красоте более глубокой, проистекающей из гармонии и согласованности воедино всех частей, которую один лишь чистый интеллект и сможет оценить. Именно эта гармония и дает основу тем красочным видимостям, в которых купаются наши чувства» [17].

Отметим, что Гильберт, прежде всего, придавал большое значение доступности и понятности математики и часто приводил слова другого математика: «Математическую теорию можно считать совершенной только тогда, когда ты сделал ее настолько ясной, что берешься изложить ее содержание первому встречному» [18].

Именно поэтому математики любят подшучивать над собой и окружающими.

Вспомним безвременно ушедшего недавно от нас математика В. Арнольда.

Свою публичную лекцию он начинал с образной классификации наук [19] по законам Мерфи: «Если воняет, то это химия, когда ничего не работает – физика, а если понять нельзя ни слова – математика».

Английский математик и почетный член АН СССР (1934) Г. Харди высокопарные слова К. Гаусса "математика – королева наук" занимательно объяснял ... полной бесполезностью обеих.

Директор Математического института (Бонн) уже в наши дни писал, что математика – это формализованное переливание из пустого в порожнее. А её вклад в решение основной проблемы человечества состоит "в отвлечении лучших умов от более опасных, чем математика, занятий". «Истинная же польза» – по его словам – в том, что если бы вместо проблемы Ферма математики занимались бы усовершенствованием автомобилей или самолетов, то вреда было бы гораздо больше» [19].

Деление всех наук на три группы «математические – естественные – гуманитарные» академик Л. Ландау переиначивал как «сверхъестественные – естественные и неестественные» [20].

Но мы немного отвлеклись...

Обратим внимание, как точно и лаконично осуществляется связь математики и гармонии у композитора М. Марутаева [21], когда он наравне с логическими аспектами рассматривает и математические начала гармонии, а само определение гармонии дает «в виде парадоксального тождества противоположностей на основе аксиоматического построения теории гармонии». Достаточно лаконично и ясно.

Математика – живой развивающийся организм. В последние десятилетия объектами математического исследования все больше становятся нечисловые объекты: события и предикаты, множества и абстрактные структуры, векторы и тензоры, матрицы и т.д.

Но опыт развития математики убеждает, что самые, казалось бы, оторванные от практики ее разделы рано или поздно находят важные применения. Во всяком случае, это её потенциальные элементы в гармонии, ибо «математика – это скелет мироздания» [22], а гармония, на наш взгляд, – его кровеносная система.

Сегодня лишь одна наука – математика – развивается внутренним путем, по этой причине главным критерием истинности математических знаний является логический критерий. Он сводится к непротиворечивости исходных посылок и результатов вывода.

Когда-то само понятие математики означало науку. И в единении знаний и систематическом мышлении изучались арифметика и музыка, геометрия и астрономия (так называемые математические науки) вместе с живописью и философией. Причем учение о музыке часто ассоциировалось с гармонией небесных сфер. Но даже в таком союзе "наука гармонии" – рудиментарное образование, которое требует иного соподчинения слов, например "научные основы гармонии".

В математике практически нет такого раздела, который так или иначе не был увязан с понятием гармонии. Практически все направления современной математики затрагивают и отражают разные аспекты гармонии в ее широком представлении (понимании).

С другой стороны, идеи гармонии уже давно вошли составляющими во многие направления современной математики: системный анализ, теория множеств, моделирование, сложные системы, геометрия, комбинаторика, алгебра и т.д.

А теперь попробуем поменять соподчиненность математики и гармонии.

Математизация гармонии. Когда мы говорим о возможной математизации гармонии, то априори подразумевается подключение к этому процессу всех средств и арсенала современной математики в зависимости от того, как и какие стороны гармонии воспроизводятся на знаковом уровне.

Действительно, опыт развития современного естествознания показывает, что на определенном этапе развития естественно научных дисциплин неизбежно происходит их математизация, результатом которой является создание логически стройных формализованных теорий и дальнейшее ускоренное развитие дисциплины.

Математизация – это характерная черта современной науки и техники, хотя точной даты начала пути математизации, пожалуй, не знает ни одна из наук.

Вот примерные печатные образы на эту тему: общая тенденция математизации наук, математизация научного знания, математизация гуманитарных знаний, математизации в естественных и социальных науках, математизация теоретической биологии и т.д.

Математизация науки обеспечивает общность формулирования законов, отражение наиболее глубоких отношений действительности, скрытых от непосредственного наблюдения. Математика – могучий инструмент познания и часто единственно возможный, когда образы ненаглядны, ненаблюдаемы, недоступны непосредственному чувственному восприятию[5].

Но гармония, наука и философия терминологически не отождествляются.

Существует и «восточная философия о мировой гармонии», к которой схема МГ не подходит в принципе. Там другие основания.

Математика не всегда располагает требуемым аппаратом для исследования абстрактной модели. Зачастую в ней приходилось открывать новые понятия и методы или разрабатывать старые, чтобы делать это.

Самого желания здесь мало. Необходимы смыслы, понятия и четкие формулировки.

Эта идея достаточно четко изложена в философском наследии Гегеля [23, с. 547]: «Дело уже не столько в мыслях. У нас их достаточно, хороших и плохих, прекрасных и смелых. Дело в понятиях. Но если мысли должны приобрести непосредственную значимость благодаря самим себе, то в качестве понятии, напротив, они должны быть сделаны понятными». – Это напрямую относится к симбиозу "М–Г".

Достаточно хорошо воспринимаемая мысль МГ на обывательском уровне становится малопонятной, когда мы её начинаем рассматривать в качестве понятия.

Одно дело броский сленг или яркий слоган, и совсем другое – строгое, понятное всем определение, с последующим очерчиванием предмета, объекта, целей и задач исследований.

Следует иметь в виду, что и плата за математизацию достаточно велика, когда начинаешь понимать, что гармония искусственного образования в принципе недостижима.

Нечто подобное присутствует в джазе, где гармонии соответствует неповторяемость в импровизации, ритм часто выпадает из механически заданного размера.

На сегодня не известно ни одного математического приложения, возникшего в результате абстрагированного рассмотрения гармонии. Все строится на базе уже развитых математических средств, которых более чем достаточно для исследования (анализа и синтеза) целостных структур. Только бери и спокойно применяй.

Поэтому выделение самостоятельной области под общим лозунгом «математики гармонии» без ясных целей и задач, предмета, области исследований, аппарата и т.п. – занятие малопродуктивное и со слабовыраженной перспективой.

Во всяком случае, очень бы не хотелось видеть в этом добром начинании некую массовку под красивым (эффектным), но малосодержательным прикрытием.

«Математика отвлекается от всего конкретного характера элементов, скрытых под ее схемами. Она делает это при помощи безразличных символов, вроде числовых или буквенных знаков» [16, гл. 2, § 3].

И если речь идет о процессе математизации гармонии, то непременно следует обозначить основные методы, в частности:

аксиоматизация – выделение компактного (конечного и простого) набора некоторых простейших утверждений (аксиом), из которых посредством логического вывода можно в принципе получить любое утверждение в области знаний о гармонии;

формализация – замена изучаемых объектов и отношений между ними наборами символов и отношений в выбранном искусственном языке (компактном, недвусмысленном и простом) и системе удобных обозначений;

математическое моделирование – отображение предметной области гармонии в математические множества (понятия, структуры) с построением математической модели на основе выделения существенных свойств и количественных характеристик гармонии и существенных отношений между ними.

Эти вопросы в рамках словесной подчиненности МГ на сегодня остаются открытыми.

И нам остается перейти от процесса математизации, как действа, к математике в гармонии, как сущностному воззрению.

Математика (в) гармонии (?). Образное понятие или словосочетание «математика гармонии» – это вся существующая и будущая математика. Нет ни одного раздела, ни одного подраздела и ни одного математического образа (объекта), которые так или иначе не связаны с широким понятием гармонии. В этом контексте с большой вероятностью МГ чревата своим парадоксальным обращением в "масло масляное", становясь математической математикой или гармонической гармонией, а может и всем сразу как «гармоническая математика математической гармонии».

Что же не хватает в своевременной математике, чтобы отдельно создавать или выделять отдельное направление?

Какой новый (полный и непротиворечивый) математический аппарат подразумевается создать? И на базе, каких новых аксиом, теорем, моделей?

Да, и нужно ли это вообще? – Вопрос не праздный. Любая теория и ее носители, как и власть, должны уметь себя не только подавать, но и защищать.

Так, русский математик Ю.В. Матиясевич спокойно решил 10-ю проблему Гильберта на основе чисел Фибоначчи, доказав алгоритмическую неразрешимость задачи о существовании решений у диофантового уравнения с произвольными неизвестными и целыми рациональными числовыми коэффициентами.

Он де-факто предъявил 10 уравнений, которые задают условие b = F_2a, где F_n – n-ое число Фибоначчи. А для этого ему пришлось доказать свойство, что F_k делится квадратом F_m тогда и только тогда, когда k делится F_m.

Например, (m, k) = (3, 18), (F_m, F_k) = (2, 2584), k/F_m = 9, F_k/F²_m = 646.

И ни о каком рождении новой математики он не упомянул ни слова.

Подобных примеров десятки тысяч.

Но даже если принять концепцию МГ, необходима наиболее реальная её оценка, например, как в работе [24]: «создание современной математической науки, как "математики гармонии", находится еще только на стадии возрождения и становления».

В целом терминологическая практика, конечно, не стоит на месте, и в повседневную или специально научную сферу внедряются все новые и новые словесные конструкции, что в целом является объективным процессом развития, а «игра с понятиями столь же обоснованна, как игра с математическими моделями» (И. Пригожин, доклад, 1997).

Если отслеживать тезис, что «современная математика отличается большой "фрагментарностью" и представляет собой набор математических теорий, не связанных общей целью», то в этом контексте вполне допустимо рассматривать гармонию или гармонизацию самой математики. А вот, наоборот, в смысле специальной доселе неизвестной математизации гармонии, – весьма и весьма неопределенно.

По Марутаеву [21] закономерности гармонии не имеют ни физико-математического, ни химико-биологического, ни иного смысла конкретных наук. Здесь смысл сущностный

Это общий закон. И его невозможно объяснить никакими уже известными законами, не говоря уже о формализованном представлении на математическом языке.

Асимметрия и симметрия, пропорция и ритм, хаос, красота и гармония…

Всё это слито воедино.

В этом смысле вся математика – числовое выражение гармонии или большое обобщенное уравнение гармонии.

Да, и прошли те времена, когда гармонию измеряли математикой.

Поэтому лучше говорить не об МГ, а о некоторой совокупности математических приемов для разрешения или описания тех или иных сторон гармонии.

Тем более что её никак нельзя отнести, ни к процессу, ни к физическому явлению.

Добавляя к математике слово "гармонии" в родительном падеже, мы тем самым даем отличительный признак определяемого понятия, желая достичь его отчетливости и определенности. Но так ли это на самом деле? – Будем рассуждать дальше.

Корни противоречий. «Подобно теории Шеннона моя "математика гармонии" описывает некоторый количественный аспект понятия "гармония", который основан на трактовке гармонии как связи и комбинации...» [13]. – Даже не сравнивая с многогранными представлениями о гармонии, которые излагались выше, здесь легко прослеживается не самое лучшее толкование гармонии с превалированием комбинаторики.

Если принять некоторое множество математических объектов за МГ, то все другие математические средства (за пределами данного множества) автоматически образуют другое множество "математики не гармонии". Что это такое можно понять только путем отрицания и только через понятие МГ, следовательно, гармония выступает в роли критерия делимости всей математики на два противоположных класса, что весьма и весьма сомнительно, исходя из онтологии математики в познании мира.

МГ не является тождественным предложением или очевидной истиной опытного знания (по Лейбницу). Но МГ нельзя отнести к научному предложению, относительно которого можно доказать, что в процессе его разложения, осмысления или развития никогда не возникнет противоречия.

Вспоминается дилемма. Является ли истинным все то, ложность чего не может быть доказана, и ложно ли все, что не может быть доказано как истинное? – А как быть тогда с тем, о чем нельзя доказать ни того ни другого?

«Существует мир гармонии, мир вечности, откуда вышли все формы, все цвета, все звуки, запахи» [22]. Но насколько сегодня "математика гармонии" системна, чтобы учитывать всеобщую взаимосвязь? – На эти вопросы математика ответить пока не может. Философский уровень рассуждений о гармонии опережает математику.

Математика (даже математика в гармонии, ввиду ее прикладного значения) – это все же анализ, разложение на части. Для синтетического видения абсолютное погружение в чистую математику в определенной мере вредно. Сегодня нужно наоборот чаще подниматься над математикой, стараясь увязывать ее со знанием других сторон бытия.

Да и как можно математикой проверить либо измерить гармонию?

Это всегда было не только забавным, но малоперспективным занятием.

Подвергшаяся математизации гармония уже несовершенна, поскольку всякая форма математики имеет свои ограничения. Да и действительный ход мысли математика совсем не обязательно бывает гармоничным.

«В математике мы можем получить некоторую относительную гармонию продукта мысли, несмотря на то, что действительное движение мысли математика не обязательно бывает гармоничным... Эта гармония несовершенна, потому что всякая форма математики, как это доказано, имеет некоторые ограничения; вот почему я называю ее только относительной» [25].

Здесь главное не сбиться на вульгарное понимание философской и математической сущности гармонии, что побуждает разнести между собой понятия математики и гармонии.

И потом не будем забывать, что гармония – это, прежде всего, «установка или базовая ценность культуры» [7] в ее широком понимании.

Поэтому "математика такой гармонии", на наш взгляд, выглядит некорректно, свидетельствует о поверхностном осмыслении философской и математической сущности гармонии, а в целом характеризуется как не совсем удачное объединение этих двух дефиниций и наиболее противоречивая по смыслу идиома из всевозможных комбинаций данных слов в их разном сослагательном наклонении.

Даже словосочетание "гармония математики" представляется более или менее выверенным, поскольку математика гармонизирует абстрактные представления и модели мироустройства.

Одной математикой гармонию не просчитаешь, «проверять алгеброй гармонию» – занятие неблагодарное. Поэтому более правильно говорить о математических методах в теории (науке) гармонии. Или в общем контексте «математика и гармония», «решение задач гармонии в математике», «математические методы в гармонии систем», «законы гармонии природы на языке математики» и т.п.

«Математика в гармонии» – это самое простое и безболезненное уточнение.

Тогда формально всю математику в гармонии можно определить через совокупность трех конечных множеств : X – элементы предметной области гармонии, R – отношений между элементами, F – функции интерпретации.

МГ–МД: «математика гармонии» – «математика дисгармонии» (?). Правильная и точно сформулированная постановка задачи – это почти половина ее решения.

Так ли это в нашем случае?

И насколько понятие МГ разгоняет облака, или наоборот затуманивает проблему?

Создавая некую структуру МГ, можно логически показать, что если в основания мы положим принцип соотнесения в состав МГ набора математических конструкций, то в ходе развертывания такой теории, мы обязательно придем к положению, когда найдутся иные конструкции, не входящие в эту структуру.

На это следует посмотреть особо. Нужно свести концы с концами в этой теории так, чтобы добиться объяснения и отражения всех аспектов гармонии.

Это задаст нам вторую группу формирующихся знаний

В ранний период развития человечества математика еще не имела такого развития, какое она получила в дальнейшем, поэтому ее удельный вес в общей системе рассуждений был невелик [15, лекция 1]. И ее можно было схематично (чисто условно) разделить на МГ–МД и таким образом охватить всю ее область. По мере развития математики уже сама формальная логика рассуждений становится одним из математических исчислений.

Но уместно также спросить: а чем будет задаваться или определяться такое деление, и чем оно сегодня оправдывается: требованиями гармонии, требованиями математики или иными критериями?

То есть мы будем выделять большую совокупность математических объектов и говорить, что все это – выражение или форма выражения гармонии.

Соответственно, оставшаяся группа подобных объектов автоматически становится выражением или формой выражения дисгармонии и т.п. Третьего здесь не дано.

Но куда, например, в таком случае мы отнесем геометрию, или топологию, либо разложение в ряд Фурье и т.п.? Каким образом мы разделим теорию чисел, чтобы ее часть отошла в МГ, а другая в математику дисгармонии?

И здесь нам очень важно не попасть в глухой лабиринт, заканчивающийся светом в тоннеле в виде рампы театра абсурдов.

Так или иначе, но «МГ как альтернативное направление в развитии математической науки» [26] просто сбивает с толку многих, кто когда-либо соприкасался с математикой.

Нужно ответить и на вопрос: а есть ли существенный разделительный рубеж между гармонией и математикой? – Не по отдельным формальным признакам, а по сути, с точки зрения характеристики и описания бытия.

И не выходит ли так, что МГ уже содержит несколько частных разделов математики или даже всю их совокупность? – И тогда у нас может получиться, как говорилось выше, "гармоническая гармония" или "математическая математика".

Кроме того, провозглашение идиомы МГ, по сути, означает строительство и новой математики, которой пока не видно. А все, что якобы сделано в рамках МГ – ничто иное как развитие отдельных уже давно существующих классических разделов математики.

Если это направление, то чем оно будет заниматься? – Изучаемые объекты, "меры весов", индикаторы и схемы сопоставления объектов и знаков, структура отношений и действий, конечный продукт анализа и т.п.

А какова логика замещения и перемещения математических объектов в системе отношений «МГ–МД»? – Вопросов больше, чем ответов.

Наличие разных, по меньшей мере, трех типов гармонии (математической, эстетической и художественной) отмечает В. Шестаков [27]. Внимание в них акцентируется соответственно на числовой соразмерности частей в целом, восприятии красоты природы и актуализации принципа гармонии в материалах искусства так, что «математическое понимание гармонии фиксирует, прежде всего, количественную определенность гармонии, но оно не заключает в себе представления об эстетическом качестве гармонии, о ее выразительности, связи с красотой».

Золотое сечение и гармония. Естественные системы в процессе самоорганизации стремятся занять свою гармоничную нишу. В своих конструкциях природа иногда использует золотое сечение (ЗС), имеющее строгое математическое (геометрическое, алгебраическое) обоснование.

Эти факты являются причиной повышенного интереса к ЗС в современной науке и являются основой для развития такого научного направления, как общая теория гармонии систем, идеи которой наиболее плодотворно развиваются в монографии [28], за исключением противоречивого вопроса обобщения математических констант.

Но разве сосновая шишка была бы менее гармонична, если бы представляла собой не проявление золотоносной спирали, а например, правильный цилиндр и кубик, а улитка – допустим, лемнискату или кардиоиду?

Разве они от этого разлетелись бы на молекулы и перестали существовать как единое целое? Конечно, нет. И в том и другом случае они сохраняют гармоническое единство и остаются ее объектом. Или разнополые люди не любили другу друга, если бы у них пупок был на уровне колен?

То есть сама по себе фиксация того или иного порядка – еще не есть гармония, даже если она "радует глаз".

Тысячи ракушек или улиток имеют в своей основе спиральные формы, совершенно не связанные с золотым сечением, но имеющие иную пропорцию частей и целого.

Подобно тому, как в музыке первичный объект гармонии – музыкальные интервалы, в геометрическом ее толковании это может быть пропорция.

Для одних гармония – это сочетание (из комбинаторики) и треугольник Паскаля.

И для такой своей гармонии они создают свою математику, в которую искренне верят и от чистого сердца проповедует.

Другие считают такой подход близоруким сужением поля (сферы) интересов гармонии, и вообще рано подвергать математизации то, что еще не вызрело в человеческой голове.

Практически все, что мы видим, чувствуем и осознаем, подпадает прямо или косвенно под еще неосознанное до конца понятие гармонии или является ее прямым проявлением, и ее нельзя загнать в жесткие рамки.

Гармония стоит на равновеликих ступеньках с методологией, философией, математикой, религией, а возможно и выше их как одна из самых значимых функций всемирного разума (целостности). Хотелось бы очень видеть бесстрашного оптимиста, отважившегося выстроить математику такой широченной глыбы.

Сводимость МГ к золотому сечению вообще сомнительна.

«Мир слишком богат, чтобы быть выраженным на одном единственном языке. Мы должны использовать ряд описаний, не сводимых друг к другу, хотя и связанных между собой тем, что технически именуется трансформациями» [29].

Именно поэтому нам диссонирует словосочетание "МГ", которое работает как полупроводник или однополюсный магнит, но не симбиоз двух мощных понятий.

Это диссонирует слух, денонсирует основания образования научных понятий и звучит в унисон с такими неестественными и вычурными формами как «математика информации» или «математика кибернетики».

Кибернетика, информация, гармония... Это важнейшие узловые точки единого синтетического ряда развивающейся науки последних лет. И они ни в коем случае не объединяются с математикой чисто механически. Поэтому человеком созданы: «математические основы кибернетики», «математическая теория информации».

Следующий логический шаг: «Математические начала (основания) гармонии».

В этой связи разумно провести краткий обзор некоторых публикаций, которые мы условно назовем МГ-литературой.

Обзор МГ–литературы. Мы уже упоминали редакционное предисловие к работе [1], что «объективно математика гармонии еще отнюдь не сформирована до такого уровня, чтобы принять канонические "учебниковые" формы».

До канонов еще действительно рановато. Возможно, даже больше 1618 метров, как в одном из поучительных сравнений: «Каждая пятилетка – это шаг к коммунизму».

Нас несколько удивляет другое.

Сколько уже прошло времени, а в публикациях до сих пор мы не находим однозначного и вразумительного представления или определения, что же собой представляет МГ?

Преимущественно встречаются отдельные мысли- высказывания о МГ:

– «альтернативное направление в развитии математической науки» [26];

– «математическое направление, которое объединяет три оригинальные математические теории в современной науке: теория чисел Фибоначчи, теория р-чисел Фибоначчи, теория металлических пропорций[6]» [30];

– «обобщения рекуррентного соотношения Фибоначчи и "золотого сечения", ... их приложения (алгоритмическая теория измерения, коды Стахова, арифметика Стахова, компьютеры Стахова, "золотая" фибоначчиева гониометрия Стахова)» [31];

– «современное математическое учение о золотой пропорции и её обобщениях» [32].

Есть и другие близкие размышления:

– "Сердцем" новой математики является "обобщенный принцип золотого сечения";

– «Математика Гармонии является развитием и обобщением тысячелетних исследований в области теории золотого сечения… Ее главная цель – ввести в современную науку золотое сечение и числа Фибоначчи в качестве фундаментальных понятий современной науки» [33].

Далее выделяются комбинаторные отношения чисел Фибоначчи, развитие алгоритмической теории измерения и систем счисления на основе p-пропорции, гиперболические функции Фибоначчи, компьютеры на основе арифметики Фибоначчи.

Вчитываясь в этот перечень, невольно ловишь себя на мысли, что он больше напоминает программу технического перевооружения вычислительной техники, все дальше и дальше удаляясь собственно от гармонии.

Конечно, очерчивать круг решаемых задач – незыблемое право исследователя.

Но это исключительно, когда он творит. После публикации результатов происходит отчуждение идеи, остается только авторство, а теория становится общим достоянием и вступает на тернистую тропу апробации-признания[7].

 Как бы то ни было, но уже из приведенного обзора наглядно видно, что интуитивно мыслимые широкие воззрения о МГ, по сути, сведены к золотой пропорции и обобщенным последовательностям Фибоначчи, как неоправданно утилитарное сужение подразумеваемой предметной деятельности.

В целом же вырисовывается довольно необычная наука, занимающаяся числами Фибоначчи, но претендующая на такую глыбу, как математизация гармонии.

Заметим, что подобные числовые ряды в природе отсутствуют[8], в то же время золотая пропорция в чистом виде встречается в спиралеобразном формировании отдельных живых образований: некоторых видов ракушек, плодов растений, подсолнечника и др. Другие примеры менее показательны, поскольку не выходят за рамки гипотез.

Вышеназванные формулировки свидетельствуют о том, что МГ еще находится в поисковом режиме, и пока это только образы или "протокол о намерениях".

Прежде всего, нет четко поставленного предмета и сформулированных задач исследования. Отсутствует также тщательный анализ самой математики, чтобы всерьез говорить об ее неисследованных направлениях, способных более компактно на формализованном уровне подвергнут гармонию математизации. Не определены главные цели, то есть чего хотят добиться, решая поставленные задачи.

Анализ других работ по данной тематике также оставляет за кадром ряд невыясненных вопросов: Какие конкретно сообщества математиков работают над этой проблемой? В каких научных журналах она освещается?

Во-первых, проблема – это положение, условие, вопрос либо объект, который создает неопределенность и затруднение, а значит, это всегда требование что-то найти, указать или построить.

Во-вторых, проблема побуждает к углубленному ее изучению и определенным конкретным действиям или их ограничениям. В частности, необходимо конкретизировать, в каком классе объектов ищется решение задачи.

Пока можно с уверенностью лишь утверждать, что проблема "МГ" – это не столько создание "красивых" математических моделей (форм) процессов и явлений окружающего мира, сколько формализованное описание отношений частей целого. При этом в качестве основного критерия выступает их соразмерность, а вовсе не грация, изящество и т.п., которые тоже имеют определенное значение, но уже вторичного плана (проявления).

Одно из немногих четких определений МГ мы находим в работах [10, 34]: «Математика гармонии – это математика, изучающая и моделирующая гармонию бытия пространственно-временных форм Жизни, их количественные отношения, проявляющиеся в эволюции природы, общества и мышления».

Формулировка в целом верная. Хотя мера (планка) уровня обобщения здесь непомерно высока, что весьма проблематично в реализации, но вполне приемлемо в философском толковании. И здесь прослеживается перекличка с А. Богдановым, который рассматривал «самую математику как ветвь всеобщей организационной науки: этим объясняется гигантская практическая сила математики как орудия организации жизни» [16, предисловие].

Но время идет, и появляются новые результаты исследований в развитии темы МГ.

Публикуются исторические экскурсы, где МГ преподносится в ракурсе, что небито наши предки, выполняя вычислительные действия, размышляли исключительно о гармонии.

Исследуя эпоху Возрождения, в работе [35] отмечается: «Если же говорить о математике гармонии, то решение кубического уравнения имеет отношение к теории уравнений, обобщающих идею золотого сечения».

С этим трудно согласиться по двум причинам.

Во-первых, разные виды кубических уравнений уже в 5 веке до н. э. решали в древней Индии, Греции и Египте, о чем подробно описано в энциклопедии [36]. То есть развитие алгебры шло своим чередом независимо от золотого сечения (ЗС), задача которого пока не ставилась, а появилась позже в Началах Евклида. И главное для чего? – «В сохранившихся древнегреческих текстах ЗС рассматривается исключительно в связи с геометрической задачей построения правильного пятиугольника в планиметрии, а также икосаэдра и додекаэдра в стереометрии с целью построения правильного пятиугольника» [37].

Во-вторых, кубическое уравнение никак не может обобщить идею ЗС, поскольку она уже давно в науке выражена через математическую пропорцию. ЗС как фундаментальная константа наоборот выделена из всевозможных алгебраических уравнений и видов пропорциональной меры, которые управляют реальной действительностью мироздания, по сути, поднявшись на пьедестал «чисел, которые изменили мир».

Константа ЗС аксиоматически не может быть обобщена, равно как величины e, π и др.

Несомненный интерес в рамках исследования тематики МГ представляет историко-математический обзор [38], задающий мажорную тональность о способности МГ исправить стратегические ошибки, допущенные в развитии математики. Автором выполнен анализ некоторых противоречий в математике и сделаны выводы в пользу МГ, хотя это больше координируется с гармонией внутри самой математики, а не наоборот.

В упомянутой работе отмечается «отсутствие четких канонических форм МГ» и представляется это даже неким плюсом в «кризисном состоянии современной математики» (?), когда в ней произошел «методологический раскол на теоретико-множественное и конструктивное направление». Вместо евклидового представления, в соответствии с которыми √2 считается иррациональным числом, от имени МГ предлагается евдоксова геометрия, «в которой √2 и многие другие дробные арифметические корни принимаются в качестве, пусть невообразимо больших, но все-таки периодических десятичных дробей».

Поднятые вопросы весьма важные и касаются первооснов математики.

Здесь очень важны не только акценты, но и интонации, когда отдельные диссонирующие ноты способны создать неповторимое слаженное звучание, возвысив саму гармонию (музыки, математики, философии и т.п.).

Поэтому выскажем некоторые соображения по поводу затронутых моментов.

1) Довольно любопытна изначальная точка зрения в такой точной науке как математика, когда четкие представления о предмете МГ видоизменяются на положительный образ об освобождении от уз догматики.

Сегодня еще рано говорить о канонах МГ, поскольку не определено главное: предмет и задачи научных исследований. Их отсутствие – и есть главный лейтмотив.

Преждевременно рассуждать о канонизации МГ, когда нет четкой концепции.

2) В качестве доказательной базы о противоречиях множественной теории Г. Кантора приводится спорная и пока не апробированная работа проф. А Зенкина [39], в которой логические построения элементарно противоречат категории обобщения в математике. В частности, из того, что мы не умеем явно предъявить еще одно число, коме диагонального, вовсе не следует, что таких чисел нет. Более подробно об этом написано в реферате [40][9].

3) Те или иные противоречия в математике были всегда. Они являлись двигателем прогресса или новых теорий и всегда спокойно разрешались силами самих математиков.

Но это имеет отношение к такому понятию как "гармония математики", а не наоборот.

Так или иначе, но математика развивается больше изнутри и способна сама разрешать возникающие несогласованности, даже не думая о том, что где-то кто-то ввел новый термин.

4) И еще одно принципиальное уточнение. Провозглашать МГ прародительницей упомянутой евдоксовой геометрии – это все равно, что «пилить сук, на котором сидишь».

Число золотого сечения обязано себе исключительно корню из пяти со всеми его миллиардами знаков после запятой в десятичном исчислении. Но стоит нам только хоть один знак изменить (пусть даже теоретически) или ввести искусственную периодичность, скажем после 10¹⁰ знака, то вся теория золотой пропорции рассыпается.

Вот простой пример, воспроизводящий модель-гипотезу большого взрыва при формировании Вселенной, где кроме самого взрыва наличествует еще и главный предварительный этап – сжатия.

В работе [41] показано, что аддитивная рекурсия двух предшествующих состояний (), как "возмущенное уравнение идеальной системы"

,

при сколь угодно малом значении  за конечное число шагов выводит систему из равновесия и приводит к бифуркации (рис. 1), .

При этом непрерывный аналог системы имеет вид , где  – комплексная функция, расширяющая последовательность Фибоначчи  на непрерывную область так, что  для целочисленных величин t=n, .

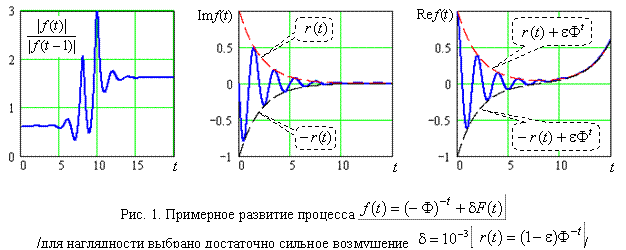
Что это может означать на практике? – Всё, где ЗС закладывается в качестве структурированной подосновы, при малейшем вмешательстве извне, вместо гармонизации подлежит деструкции (взрыву или распаду), то есть конструкции ЗС неустойчивы.

Но по такой же схеме тогда может рассыпаться и сама теория МГ, в основе которой лежит ЗС.

В рамках теории, близкой к философскому смыслу МГ, нам наоборот необходимо наличие абсолюта в виде корня из пяти, а уже для алгоритмических схем измерения можно принимать любую приемлемую или инструментально-достижимую точность вычисления.

И даже не нужно задумываться о сути замечательных работ знаменитого немецкого математика Георга Кантора, который родился (1845) и 11 лет прожил в Санкт-Петербурге.

А если он в чем-то и ошибался, то подобного рода творческие ошибки можно пожелать многим ныне ищущим ученым.

Кстати, Г. Кантор определил множество как «единое имя для совокупности всех объектов, обладающих данным свойством», что очень близко к формализованному описанию гармонии. Математикам-гармонистам есть повод об этом подумать.

Так что рано сбрасывать со счетов этого великого ученого, который презентовал миру также теоретическую подоснову фракталов через образ "канторовой пыли" и еще много чего полезного на стыке "математика–гармония".

Но пойдем дальше...

Обстоятельный и разноплановый ответ по вопросу словообразующей формы МГ представлен в работе [42]. Составлена достаточно четкая классификация по сопоставимости понятий математика–гармония. Хотя она содержит только необходимый, но не достаточный набор признаков соотнесения гармонии по приведенной градации.

Есть и другое "но".

Выстраивание ряда является неубедительным, поскольку всё озвученное – составные части самой гармонии, которая является не элементом данного ряда, а его порождающим началом, как, впрочем, и многих других понятийных форм.

Возьмем ту же биологию, экологию, космологию, и даже физику и химию. Разве все то, что является предметом их изучения, не подпадает под понятие гармонии, которая здесь является самостоятельной полноправной наукой и даже наднаукой?

Все хорошо, если мы располагаем точным однозначным определением и целостным учением о гармонии. Тогда находим ей свою нишу в классификации проф. Мартыненко и все в порядке. Но в том-то и дело, что этого пока нет и в помине. Мы только вначале пути.

Сравните разноликие определения гармонии, и Вы сразу это почувствуете.

Несмотря на интуитивно понятное представление связки «математика–гармония», не исключено, что она может оказаться орешком, посильнее времени. Просто за нее, кроме музыкантов и теоретиков-музыковедов, серьезно еще не брались.

Или попробуйте ответить на, казалось бы, простой вопрос: как осуществляется гармония времени, пространства и материи? Или как математически выписать гармонию теории и практики, гармонии науки и религии?

Поэтому рано говорить о смыслах МГ, до конца не понимая самой гармонии.

А так получается, что еще нет стройного учения о гармонии, а ей уже выделили [42] место. И главное где? – Среди ритмики и грации (?).

Но не сужаем ли мы тем самым рамки рассмотрения такого феномена? – Возможно, это метанаука. А на наш взгляд, даже нечто более размашистое и объемлющее.

И более значимыми по иерархии здесь могут быть только категории пространства и времени. Но даже они не мыслимы и не существуют без их увязки через понятие гармонии.

«Демон гармонии» еще более вездесущий, чем демон Лапласа.

Попробуйте назвать или представить что-нибудь отдаленное или несвязанное с гармонией в ее широком представлении. Весьма трудное и бесперспективное занятие.

А чем можно объяснить закон Бела, кроме как гармонией мира?

А как можно описать единство и многообразие бытия без его гармонии?

Но может, кто-то попробует научно обосновать, что кризис выпадает из обоймы гармонии? – Как раз наоборот, кризис – это самоочищение в гармонии.

Хаос – тоже часть гармонии, только слабо организованная! Ибо хаос – противоположность организованности бытия по неким законам. С точки зрения, как диалектики, так и триалектики, гармония – единство хаоса и организованности. Вопрос в том, чего больше и в каких границах количественных отношений.

И коль мы уже затронули философские мотивы МГ, то трудно обойти стороной высоко содержательные статьи [1, 32] – автора интеллектуально-художественного произведений "ковры Абачиева" – многоцветные фрактальные структуры в треугольнике Паскаля.

Он провел большой объем исследований о становлении и развитии алгоритмической теории измерений и кодов Фибоначчи, формально без какого-либо анализа принимая (больше на веру), что это и есть МГ.

Исходя из логики этих работ, нельзя не заметить, что некоторые модели МГ вышли из недр треугольника Паскаля как его фрактальные образования (р-сечения), а вот самим фракталам, как, впрочем, и многим другим "гармонизированным" направлениям современной математики, в МГ пока места не нашлось.

Это наводит на мысль, что у направления МГ имеется запас прочности и есть будущее.

Только необходим небольшой косметический ремонт самого наименования и предметной платформы, чему мы собственно и посвятили свои рассуждения.

«Название новой научной дисциплины – дело особо ответственное. Это – "одежка", по которой широкая научная общественность её встречает, и по ней же склонна выпроваживать, не вникая в её "ум"... Термин МГ в учении о золотой пропорции не из тех, которым простительны даже небольшие расхождение со смыслом понятия, а тем более – такие, которые фактически придают математике философский смысл и вызывают подозрения в её философских притязаниях» [32]. И далее автором предлагается обсудить терминологическую конструкцию «математические основания гармонии».

По нашему разумению, этот вопрос стоит внимания. Тем более что в свое время он остался неразрешенным ввиду взаимного нежелания прислушаться к аргументации сторон.

Следует отметить, что на наши замечания [2] была ответная конструктивная критика [43]. Усиливая собственные доказательные позиции и аргументацию, автор столь широко нарисовал картинную мозаику понятия "гармонии", что, видимо, и у самого закралось сомнение о практических возможностях математики описать все стороны такого объемного и разностороннего понятия, разве что привлечь для этого всю математику вообще, а не только ее золотоносную часть в виде МГ.

Пифагорейские мотивы гармонии сфер. Иногда в рамках поднятия рейтинга МГ довольно экспрессивно рассуждают о "возрождении пифагорейской математики"[10].

Доподлинно известно, что сам Пифагор не написал ни строчки, хотя Рафаэль Санти в своей знаменитой картине "Афинская школа" и представил его что-то пишущего, а все, что донесли ученики-пифагорейцы, уже нашло свое отражение в математике.

Что же тогда восстанавливать?

а) Возможно, речь идет о философски-эзотерической абсолютизации числа в мироздании? – Но в этом направлении работа специалистов не прекращается, и по сей день. Литературно-интернетовский эфир просто изобилует числовыми интерпретациями нумерологии на любой вкус: "от родиться – до умереть". Но встречаются и вполне основательные исследования, например на сайте "Числонавтика" А. Корнеева.

Правда методология, идеи и методы официальной теории чисел куда более значимы, убедительны и системны. Во всяком случае, пока.

б) А может, имеется в виду исследование истоков "промышленного шпионажа"? – Тогда, неплохо познакомить широкую общественность, включая школьников, что «теорема Пифагора была опубликована (в Вавилоне клинописью) за пару тысяч лет до него, вместе с доказательством и с формулой для нахождения Пифагоровых троек (вроде 3² + 4² = 5²), описывающих все прямоугольные треугольники с целыми длинами сторон» [44].

Или как в пифагорейской школе была засекречена несоизмеримость диагонали квадрата с его стороной (то есть иррациональности числа Ö2). «Этот факт подрывал значение арифметической теории дробей (и тем самым всей математики): дроби оказывались недостаточными для потребностей физики (для измерения всевозможных длин), а, следовательно, математики занимаются ненужной чепухой, их следует прогнать или, по меньшей мере, не кормить» [44].

Непростую задачу по добавлению к арифметике дробей новой науки в виде теории вещественных чисел блестяще решил Евдокс Книдский (воспитанник школы Платона), который в дополнение к числам ввел более широкое понятие геометрической величины, то есть длины отрезка, площади или объема, а также дал аксиоматику для сравнения величин.

в) Но ближе всего к математике того времени, пожалуй, стала гармония сфер.

Действительно, это «учение восходит еще к Пифагору и объединяет вместе математику, музыку, и астрономию. В сущности, небесные тела, будучи большими объектами, в своем движении должны продуцировать музыку. Совершенствование небесного мира требует, чтобы эта музыка была гармоничной, но это скрыто от наших ушей только потому, что всегда присутствует. Математика гармонии была центральным открытием огромной важности для пифагорейцев» [45, с. 160].

В процитированном оксфордском философском словаре (1994) одного автора мы видим словосочетание МГ, которое даже могло бы претендовать на первенство введения термина, подразумевающего симбиоз математики, музыки и астрономии. Но достаточно беглого взгляда чтобы понять: в контексте лично-авторского изложения МГ выступает в виде чисто философско-литературного образа пифагорейцев при описании ими музыкальной гармонии сфер, но не научное понятие, в том числе самой математики.

Однако что-либо возрождать в контексте гармонии сфер все равно не приходится, поскольку всё уже давно донесено до современного читателя, а также нашло новое развитие в работах А. Марутаева с его мыслительно-музыкальным восприятием мира. Кстати, именно он, можно сказать впервые, предложил в свое время термин-направление "математические начала гармонии"[11] [21], который позже стал переиначиваться и видоизменяться разными авторами (часто без ссылок), в том числе трансформируясь в его бесформенный образ МГ.

И коль мы заговорили об использовании выражения "МГ" в литературе, уместно упомянуть еще один источник (других, пожалуй, больше и нет), где говорится о единении математики и гармонии у древних греков, что до сих пор является вдохновляющей моделью для современных ученых [46, с. 65]. Именно для такого единения автор действительно использует английское написание "Mathematics of Harmony". Но это чисто образное сленговое словосочетание в книге, необыкновенно далекой от математики и посвященной социальной теме. Из общего прочтения видно, что никакой это не термин, а чисто газетный слог и единственное на 124 страницах употребление автором (дабы не повторяться) такого выражения – в контексте единения математики и гармонии. Уже далее (с. 69) он отмечает, что «Гармония имеет математические и нематематические измерения».

Вместо заключения. Проведенный анализ позволяет сделать ряд высказываний.

Какой-либо особой и отдельно взятой математики, написанной для отображения гармонии, сегодня не существует. Во всяком случае, в математических кругах о ней ничего не известно. В многовековой истории математики также отсутствуют какие-либо малейшие попытки составлять (обустраивать) отдельные подразделы, связанные с гармонией.

Более того, подобные вопросы никогда и никем из профи-математиков не поднимались, а наши альтернативные высказывания на эту тему, можно сказать первые, и фактически выступают в роли лифта, поднимающего на контрастах сами идеи МГ.

Но будем исходить из реалий и научных традиций, давая себе отчет в том, что в чистом виде вряд ли родится такой самостоятельный математический аппарат.

Это все равно, что создавать математику бытия, математику тектологии, алгебру информации, арифметику философии или методологии.

Сомневающимся хотим предложить назвать хотя бы один раздел математики, целиком обособленный от теории гармонии, то есть не имеющий к ней прямого или косвенного отношения. Мы пытались, у нас не получилось.

Да и сама по себе математика никогда не являлась основой какой-либо отдельно взятой науки. В этом контексте "математика гармонии" – рудимент, как зачаток или начальная форма, требующие своего дальнейшего осмысления, развития и самое главное – внедрения в научный мир непротиворечивой и понятийно-недвусмысленной терминологии.

В подогнанной одёжке, не обязательно с золотыми пуговицами, у нее будет будущее.

Гармония – это сочетание элементов, которое в частности, может вызывать ощущение красоты. Но гармония не сводится исключительно к красоте или созвучности.

Гармония – это и разные соотношения между большим и малым, которые например, могут выражаться "золотым" сечением (ЗС). Но гармония не сводится только к ЗС.

Гармония – это симметрия и изоморфизм, равновесие и ритмика, периодичность и т.п.

Сюда можно добавить баланс и уравновешенность, хаос и организованность, сложность и простоту, полноту и целостность, единство и контрасты и т.п., а также практически все, что свойственно системному анализу и синтезу противоположностей целостности во всех материальных и идеальных явлениях бытия действительности.

Гармония – это все и ничего. В смысле – все сразу и вместе – в общем, и конкретно, но отдельными кусками, – в частном.

Сначала нужно научно определить приоритетные направления теоретической и прикладной математики, требующие проблемного развития для решения специфических задач (если таковые имеются) и совершенствования теории гармонии.

Ответы на данные вопросы должны быть системно обусловленными и научно-обоснованными, чтобы здоровая идея симбиоза математики и гармонии не превратилась в радужный, но недолговечный мыльный пузырь.

Чтобы не натыкаться на стену непонимания в виде адекватных суждений: «Создана и развита до современных знаний не математика гармонии, а утилитарная математика, обслуживающая жизненно-материальные запросы цивилизации и игнорирующая законы гармонии Космоса» [34].

Чтобы не получались лингвистические конструкции как у отечественного языковеда Льва Щербы[12]: «Глокая куздра штеко будланула бокра и курдячит бокренка» [17].

Предлагается подумать и о теме творческого проекта в общем контексте «математика и гармония», когда вполне допустимо использовать МГ как рабочий проект или условное название. Хотя по нашему мнению, сокращенный (укороченный) термин МГ, с претензией на альтернативу или пока еще слабо аргументированную новую парадигму, до известной степени выступает диссонансом в преемственности связей между прошлым и будущим процесса развития человеческих знаний, что все-таки ближе воззрениям о дисгармонии.

Мы высказали свои соображения, а дальше каждый вправе называть предмет обсуждения на свой лад.

Но неплохо было бы одновременно направить толику своих многогранных знаний на постройку храма-учения самой гармонии, открыв новый виток начал (после Евклида и Ньютона), но уже в увязке с гармонией мироздания.

Послесловие. Кто-то обязательно захочет нас упрекнуть в отсутствии конструктивных предложений.

Сразу заметим, что мы и не ставили такой задачи.

Это прерогатива разработчиков теории.

Но подобные предложения автоматически появляются из контекста сказанного, если между словами "математика–гармония" вставить любые подходящие связующие линии.

А в том, что они напрашиваются, уже нет никаких сомнений.

В такой постановке вопроса нам не нужно будет давать определение МГ, устанавливать границы применимости, выделять "гармонизирующие" разделы математики, отсекая не понравившиеся и т.п.

Достаточно просто означить интересуемые признаки гармонии и описывать их на математическом языке.

Можно и наоборот: имеющиеся или новые математические закономерности распространять на изучаемые стороны гармонии.

В добрый путь к новым знаниям,

очные и заочные участники 1-го Международного конгресса

по математическим проблемам гармонии!

С пожеланием не заблудиться на математических просторах гармонии.

А наши мысли, надеемся, станут в этом Вам хорошим подспорьем или просто полезными вешками-указателями.

Литература.

1. Абачиев С.К. Математика гармонии глазами историка и методолога науки // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15991, 11.07.2010. – http://www.trinitas.ru/rus/doc/0232/009a/02321185.htm.

2. Василенко С.Л. Геометрические образы и закономерности гармонии // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15445, 01.08.2009. – http://www.trinitas.ru/rus/doc/0232/009a/02321141.htm.

3. Davidson D. The Method of Truth in Methaphysics // Inquiries into Truth and Interpretation. – Oxford, 1985. – Р. 199–214. – http://filosof.historic.ru/books/c0014_3.shtml.

4. Черепахин Ю. Философско-математическое осмысление природы человеческой гармонии. – 2006. – http://feano.yorik.su/attach/17/6235.doc.

5. Борзова Е.П. Триадология. – СПб.: СПбГУКИ, 2007. – 672 с.

6. Лосев А.Ф. Гармония // Большая советская энциклопедия: 3-е изд. Т. 6. – М.: Изд. "Сов. энц.", 1971.

7. История философии: Энциклопедия / Составитель и гл. научный редактор А.А. Грицанов. – Минск: Книжный Дом, 2002. – 1376 с.

8. Философский энциклопедический словарь / Ред. сост.: Губский Е.Ф., Кораблева Г.В., Лутченко В.А. и др. – М.: Инфра-М, 2003. – 576 с.

9. Миронова Л.Н., Иванов Д.Г. Теория гармонии. – 2008. – http://mironovacolor.org/theory/harmony_theory/#.

10. Всемiром. Определения. Физические и иные основы нового мировоззрения // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.14954, 14.12.2008. – http://www.trinitas.ru/rus/doc/0226/003a/02261002.htm.

11. Алферов С.А. Путь Мира // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15614, 24.10.2009. – http://www.trinitas.ru/rus/doc/0016/001c/00161564.htm.

12. Маркс К., Энгельс Ф. Сочинения: 2-е изд. Т. 20. – М.: Госполитиздат, 1961. – 824 с.

13. Стахов А.П. О статье П.Я. Сергиенко «Триалектика о началах метагеометрии и математике гаромонии» // Академия Тринитаризма. – М.: – Эл. № 77-6567, публ.12297, 27.07.2005. – http://trinitas.ru/rus/doc/0016/001b/00160183.htm.

14. Декарт Р. Правила для руководства ума // Декарт. Соч. в 2-х т. Т.1. – М.: Мысль, 1989. – С. 77–153.

15. Щедровицкий Г.П. Процессы и структуры в мышлении. Курс лекций. – М.: Путь, 2003.

16. Богданов А.А. Тектология. Всеобщая организация науки. / Под ред. Л.И. Абалкина. – М.: Экономика, 1989. – Т. 1. – 304 с.

17. Успенский В.А.[13] Апология математики, или о математике как части духовной культуры // Новый Мир. – 2007. – № 11–12.

18. Болибрух А.А. Проблемы Гильберта (100 лет спустя). – М.: МЦ НМО, 1999. – 24 с.

19. Арнольд В.И. Публичная лекция 13 мая 2006 года. – http://elementy.ru/lib/430178/430281.

20. Яглом И.М. Что такое математика // Квант. – 1992. – № 9. – С. 3–8.

21. Марутаев М.А. Гармония мироздания // Сознание и физическая реальность. – 1997. –№ 2(4). – С. 35–52.

22. Шадрин В. Гармония – глазами не математика // Грани эпохи. – 2009. – № 37. – http://grani.agni-age.net/articles9/3722.htm.

23. Гегель Г.В.Ф. Работы разных лет. В 2-х томах. Т.2. – М.: Мысль, 1971.– 630 с.

24. Сергиенко П.Я. Глобальный проект Математики Гармонии // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.14163, 23.01.2007. – http://www.trinitas.ru/rus/doc/0016/001b/00161331.htm.

25. О разуме // О самом важном. Беседы Джидду Кришнамурти с Дэвидом Бомом: Пер. с англ. Т.Богатыревой. – 1996. – http://lib.uka.ru/lib2/10/KRISHNAMURTI/oglawnom.html.

26. Стахов А.П. Три "ключевые" проблемы математики на этапе ее зарождения и "Математика Гармонии" как альтернативное направление в развитии математической науки // Академия Тринитаризма. – М.: – Эл. № 77-6567, публ.15507, 04.09.2009. – http://www.trinitas.ru/rus/doc/0232/004a/02321098.htm.

27. Шестаков В.П. Гармония как эстетическая категория: Учение о гармонии в истории эстетической мысли. – М.: Наука, 1973. – 256 с.

28. Сороко Э.М. Золотые сечения, процессы самоорганизации и эволюции систем. Введение в общую теорию гармонии систем: Изд. 2-е. – М.: URSS, 2006. – 262 с.

29. Пригожин И., Стенгерс И. Порядок из хаоса. Новый диалог человека с природой: Пер. с англ. – М.: Прогресс, 1986. – 432 с.

30. Стахов А.П. Что такое «Математика Гармонии»? (к публикации книги П.Я. Сергиенко «Триалектика. Начала математики гармоничного мира. (Русский проект)» // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15358, 22.06.2009. – http://www.trinitas.ru/rus/doc/0232/009a/02321125.htm.

31. Стахов А.П. Обобщения задачи о кроликах, чисел Фибоначчи и Золотого Сечения // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15310, 28.05.2009. – http://trinitas.ru/rus/doc/0232/012a/02322076.htm.

32. Абачиев С.К. Математика гармонии: от разработки "по горизонтали" к разработке "по вертикали" // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.16008, 22.07.2010. – http://www.trinitas.ru/rus/doc/0232/009a/02321188.htm.

33. Стахов А.П. Математика Гармонии как новое междисциплинарное направление современной науки // Академия Тринитаризма. – М.: Эл № 77-6567, публ.12371, 19.08.2005. – http://www.trinitas.ru/rus/doc/0232/004a/02320001.htm.

34. Сергиенко П.Я. Триалектика. Начала математики гармоничного мира. (Русский проект) // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15356, 21.06.2009. – http://www.trinitas.ru/rus/doc/0232/009a/02321124.htm.

35. Мартыненко Г.Я. Математика Гармонии: Возрождение (XIV–XVI вв.) (к 500-летию книги Луки Пачоли «О божественной пропорции») // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.16006, 20.07.2010. – http://www.trinitas.ru/rus/doc/0016/001c/00161679.htm.

36. Cubic function // From Wikipedia, the free encyclopedia. – 18.07.2010. – http://en.wikipedia.org/wiki/Cubic_function.

37. Щетников А.И. Золотое сечение, квадратные корни и пропорции пирамид в Гизе // Математическое образование. – 2006. – № 3 (38). – С. 59–71. – http://www.nsu.ru/classics/pythagoras/Pyramis.pdf.

38. Клещев Д. Исторические корни аксиоматических противоречий и Математика Гармонии // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.16005, 20.07.2010. – http://www.trinitas.ru/rus/doc/0232/009a/02321187.htm.

39. Зенкин А.А. Ошибка Георга Кантора // Вопросы философии. – 2000. – № 2. – С.165–168.

40. Станишевский О.Б. Апология Бесконечности в связи с парадоксом "Лжец". – http://www.roman.by/r-7271.html.

41. Василенко С.Л. Бифуркации в нелинейной динамической модели, основанной на "золотой" пропорции // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15232, 14.04.2009. – http://www.trinitas.ru/rus/doc/0232/012a/02322037.htm.

42. Мартыненко Г.Я. Еще раз о термине «Математика гармонии» (взгляд лингвиста) // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15503, 02.09.2009. – http://www.trinitas.ru/rus/doc/0232/009a/02321153.htm.

43. Мещеряков В. Математика Гармонии. Реплика // Академия Тринитаризма. – М.: Эл. № 77-6567, публ.15475, 16.08.2009. – http://www.trinitas.ru/rus/doc/0021/001a/00211107.htm.

44. Арнольд В.И. Математическая дуэль вокруг Бурбаки // Вестник РАН. – 2002. – Т. 72, № 3. – С. 245–250. – http://www.mccme.ru/edu/index.php?ikey=viarn_burbaki.

45. Blackburn S. The Oxford Dictionary of Philosophy. – New York: Oxford University Press, 1994, 2005. – 408 p.

46. Dimitrov V. A New Kind of Social Science: Study of Self-organization of Human Dynamics. – Morrisville: Lulu press, 2005. – 112 р.

© Василенко, Сергиенко, 2010

---

[1] Известен диалог Платона "Парменид" о беседе 65-летнего Парменида, 40-летнего Зенона, 20-летнего Сократа и юноши Аристотеля (не имеющего отношения к одноименному философу).

[2] Аксиология (греч. axia – ценность, logos – слово, учение) – философская дисциплина, занимающаяся исследованием природы ценностей как смыслообразующих оснований человеческого бытия, которые задают направленность и мотивацию человеческой жизни, деятельности и конкретным деяниям и поступкам.

[3] http://www.edudic.ru/dal/5625.

[4] Эстетика: В 4-х т., Т. 1. – М.: Искусство, 1968. – с. 149.

[5] Большая энциклопедия нефти и газа. – http://www.ngpedia.ru/id233306p1.html.

[6] Речь идет о квадратном уравнении, изучаемом в школе.

[7] Апробация (лат. approbatio) – это одобрение, обычно официальное. Часто с апробацией путают публичное выступление на конференции, семинаре и т.п. Сам по себе доклад – еще не апробация. Оное происходит после одобрения научной общественностью.

[8] Часто говорят, что семена подсолнечника располагаются по спиралям. А их количество по двум направлениям, якобы составляет 34/55 или 89/144. Это не совсем верно. Спираль всего лишь одна! В ее основе лежит золотой угол (~137,5^о), и она свободно воспроизводится простым моделированием. Остальное – издержки зрительного восприятия и способности человеческого глаза улавливать отдельные линии.

[9] «Отвергать актуальную бесконечность и канторовскую теорию множеств на том основании, что и диагональный метод доказательства существования бесконечных множеств, больших по своей мощности, чем счетное множество натуральных чисел, и само счетное множество как начальная актуальная бесконечность являются противоречивыми, – занятие несостоятельное и бесперспективное... Противоречия канторовской теории множеств устранимы, и условиями их устранения является строгое соблюдение законов и принципов классической логики, как в конечном, так и в бесконечном».

[10] http://www.trinitas.ru/rus/doc/0232/009a/02321189.htm.

[11] Впервые предложено в книге (с. 130–233, гл. 2): Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение. Три взгляда на природу гармонии. – М.: Стройиздат, 1990. – 343 с.

[12] Точная фраза академика Л.В. Щербы неизвестна, сам же он произносил ее в разное время по-разному, а потому верификация изначального варианта, судя по всему, невозможна. Фраза создана для иллюстрации того, что многие семантические признаки слова можно понять из его морфологии (формы и строения).

[13] Успенский Владимир Андреевич – доктор физ.-мат. наук, проф., зав. каф. математической логики и теории алгоритмов механико-математического факультета МГУ им. М.В. Ломоносова.