2.2. "Пространство" ССЦ и особенности его организации 

 

 

Согласно ОТС Ю.А.Урманцева [137] суть первого закона  преобразования композиции системы состоит в следующем. Для системы  возникновение подмножеств возможно в том и только в том случае,  когда при преобразовании композиций одних подмножеств  композиции  других подмножеств изменяются: 1) только число, 2) только  отношения, 3) число и отношения между первичными элементами 4)  первичные элементы, 5) число и первичные элементы, 6) отношения и  первичные элементы, 7) число, отношения и первичные элементы. Этот  закон позволяет заключить, что только семью различными способами  Природа может творить свои объекты. Сущность закона следует из  того, что все композиции системы порождаются из первичных элементов  множества, отобранных по некоторому основанию (в нашем случае  "противоположности" в структурах сердечного цикла). .А.Урманцев  показал, что каждый объект суть система и обязательно должен  принадлежать хотя бы одной системе объектов того же рода  (R-системе) [136, 137]. Причем каждый из объектов-систем построен  из всех или части одних и тех же "первичных" элементов в  соответствии с частью или со всеми отношениями и законами  композиции, реализованными на рассматриваемой системе объектов  данного рода. Представление объектов в системе объектов того же  рода имеет огромное значение, поскольку позволяет выявить такие  аспекты организации R-систем как полиморфизм, изоморфизм,  симметрия, асимметрия и ряд тесно с ними связанных явлений. По этой  причине необходимо в краткой форме дать представление категорий  "полиморфизм", "изоморфизм", "симметрия". 

По определению, данному Ю.А.Урманцевым, "полиморфизм - множество объектов, построенных из р элементов по n, или множество  объектов, различающихся по составу и/или отношению между  элементами" [136, с. 66]. Очевидна аналогия полиморфии с  размещениями, поскольку размещения - это соединения, составленные  из p элементов по n различных элементов и отличающиеся друг от  друга или каким-то элементом или порядком элементов. Иначе говоря,  с математической точки зрения полиморфическая модификация - это  просто размещение, а полиморфия - множество размещений. 

Изоморфизм двух или нескольких множеств заключается в том, что  между их элементами по какому-либо закону существует  взаимно-однозначное соответствие. В этом случае каждое из множеств  называется изоморфным образом других. Частным случаем изоморфизма  является автоморфизм - взаимно-однозначное отображение системы  объектов с заданными отношениями на самое себя. 

Согласно определению Ю.А.Урманцева, "Симметрия - это  категория, обозначающая сохранение признаков П объекта О  относительно изменений И" [136]. Поскольку относительно другой  совокупности изменений рассматриваемое множество признаков П не  будет инвариантным, то необходимое дополнение любой симметрии -  соответствующая ей асимметрия. Важно отметить, что симметрия  является частным случаем полиморфии, когда полиморфные объекты  полностью состоят из одних и тех же элементов, а законы  преобразования всех элементов одинаковы. Симметрия является также  частным случаем изоморфии, когда имеет место отображение объекта на  самого себя.

 

2.2.1. "Геометрическое" представление "пространства"  и системы объектов одного и того же рода

 

Вернемся к "пространству" (2.7) и покажем, что оно является  объект-системой. В этой системе первичными элементами следует  принять множество ССЦ по основанию их "существования" в условиях  физической нагрузки. Отношением единства этих элементов является  то, что они относятся к животным одного класса - млекопитающим.  Законом композиции системы является выражение (2.7). В обобщенном  законе (2.7) представлены переменные величины k_j, a_j, b_j, d и W_i ,  связанные со сменой параметра, уровня нагрузки и веса животных.  Поскольку для каждого _j-параметра величине k_j соответствуют "свои"  значения a_j и b_j , то для удобства анализа все разнообразие ССЦ можно связать с изменениями k_j,  d и W_i . В таком случае по аналогии  с геометрией выражение (2.7) можно представить трехмерным  "пространством" с "координатами" k_j, d и W, соответственно  представляющими параметр, нагрузку и вес (рис. 2.1). Отдельную ССЦ  в этом "пространстве" можно считать "точкой".

Согласно варианту ОТС Ю.А.Урманцева [136] всякая ССЦ  некоторого параметра должна являться, с одной стороны,  представителем "своего" полиморфического множества, а с  другой стороны, изоморфична опреде-

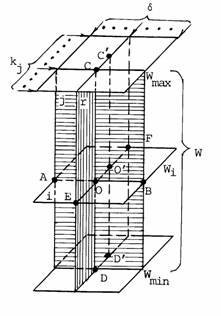
Рис. 2.1. "Пространственное" представление структур сердечного  цикла (ССЦ) в соответствии с (2.7): k_j - фактор сердечной  деятельности, d - уровень относительного кровоснабжения организма,  1£d£4; W - вес животных, W_min £W£W_max , где W_min, W_max-  соответственно минимальный и максимальный веса животных. Объект О -  ССЦ с "координатами" k_j=h, W=W_i, d=d_r; j - "плоскость"  полиморфизмов, r - "плоскость" изоморфизмов, i - функциональная  "плоскость"; AB - система полиморфичных объектов одного и того же  рода; CD - система симметричных объектов одного и того же рода; EF  - система изоморфичных объектов одного и того же рода; С`D` -  система симметричных объектов одного и того же рода, куда объект O`  входит в качестве объекта того же рода (k<sub>j</sub>=h`, W=W_i, d=d_r). 

 

деленным ССЦ полиморфических множеств,  представляющих другие параметры. Кроме того, та же ССЦ должна быть  симметрична определенным ССЦ в других полиморфических множествах  аналогичного параметра. Эту взаимосвязь можно легко показать,  исходя из "геометрического" представления "пространства" (2.7).  Нами было показано [152], что всякая ССЦ с некоторыми заданными  "координатами" k_j =h, W=W_i и d=d_r ("точка" О, рис. 2. 1) принадлежит  к трем различным системам одного и того же рода (R-системам). В  качестве первой R-системы выступает R^(П) -система, т.е. система  полиморфичных друг другу j-ССЦ отдельного i-животного (W=W_i ) в  пределах вариации нагрузки (d=1-4) ("линия" АВ, рис. 2.1).  R^(П) -система является ничем иным как совокупностью j-ССЦ отдельного  животного при всех уровнях нагрузки. Второй системой объектов  одного и того же рода, в которую входит ССЦ, является  R^(С) -система, т.е. система симметричных j-ССЦ при заданной величине  d=d_r для множества животных (W_min£W£W_max) ("линия" CD). Третьей  системой является R^(И) -система. Эта система представляет собою  изоморфную совокупность ССЦ всех рассматриваемых параметров для  отдельного животного при заданном уровне физической нагрузки (d=d_r,  "линия" EF). (Индексы "п", "и" и "с" указывают на специфику  преобразования объектов R-систем - полиморфную (п), изоморфную (и)  или симметрийную (с).) Таким образом, исходя из закона (2.7), нами  установлена принадлежность любого объекта "пространства" к "своим"  R-системам полиморфических, изоморфических и симметричных объектов.  Как следствие этого, очевидно "пересечение" аспектов полиморфии,  изоморфии и симметрии в каждом объекте (ССЦ), проявляющееся в  принадлежности ССЦ сразу к трем R- системам. В "пространстве" (2.7)  полиморфичность объектов R^(П) -системы связана с изменением  нагрузки, изоморфичность объектов R^(И)-системы - со сменой  параметра и симметрийность объектов R^(С) -системы - с изменением  веса.

 

2.2.2. Законы преобразования R-систем

 

Полиморфическое преобразование объектов R -системы по  отношению к рассматриваемому объекту (j-ССЦ) в "пространстве" (2.7)  происходит по законам [152] 

 

,                                (2.10) 

 

,                               (2.11)

 

  ,                                (2.12) 

 

где  ,   и    - соответственно законы  полиморфического преобразования систолического, диастолического и  суммарного элементов j-ССЦ отдельного животного в пределах  изменения нагрузки. Как видно из выражений (2.10)-(2.12), законы  преобразований полиморфических объектов отдельного животного не связаны с его весом, т.е. являются общими для всех животных.

Законы изоморфического преобразования одинаковы и для  систолического, и диастолического, и суммарного элементов j-ССЦ.  Преобразование объектов R^(И) -системы по отношению к заданной j-ССЦ  происходит в соответствии с законом [152] 

 

,           (2.13) 

 

где индекс j` указывает на ряд изоморфических объектов с различными  значениями k<sub>j’</sub> , a<sub>j’</sub> и b<sub>j’</sub> (например, объект О`, рис. 2 1). 

Преобразование объектов R^(С) -системы по отношению к  рассматриваемому объекту осуществляется в соответствии с законом  [152, 281] 

 

r_j^(C)= (W/W_i) .                            (2.14) 

 

R^(C) -система представляет собою совокупность ССЦ некоторого  j-параметра для множества животных при одной и той же величине d=d_r . Очевидно, что выражение (2.14) является неизменным для любой  величины d. Особо следует отметить, что в золотом режиме  кровоснабжения, т.е. при d=d_зс =1, в объектах R^(С) -системы имеет  место двойная симметрия: 1) аффинная симметрия (по золотому  сечению) "внутри" каждого объекта в отдельности и 2) симметрия ряда  "золотых" объектов по закону (2.14). В первом случае симметрия  представлена пропорцией, а во втором - группой преобразований.  Симметрийная R-система, соответствующая золотому сечению,  представляет наиболее экономичный режим кровоснабжения организма  для всех млекопитающих [152]. 

 

2.2.3. Группа преобразований "точечных" объектов "пространства" 

 

R^(П) -система отдельного i-животного по закону (2.14) может  быть преобразована в симметричные ей R^(П)-системы других  животных. Эти системы на рис. 2.1 представлены "линиями",  параллельными АВ. Как следствие этого, получаем å_С R^(П) -систему, где  в качестве симметрийных объектов того же рода выступают отдельные  R^(П) -системы; символ å_С обозначает множество симметричных R^(П)-систем. Инвариантами для данной симметрийной системы, имеющими  место для всех животных в пределах изменения нагрузки, являются  величины [280]

 

            n_s = 0,382Öd,                                                                             (2.15)

               n_d = 0,618/Öd,                                                                           (2.16) 

 

где n_s(d), n_d(d) - соответственно отношения систолической и  диастолической величин j-параметра к их сумме в пределах  изменения d=1-4 (рис. 2.2). 

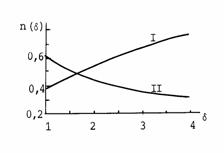
Рис. 2.2. Инварианты структур сердечного цикла (ССЦ) в  условиях относительного крово-снабжения организма; d - уровень  относительного кровоснабжения организма по отношению к золотому  режиму крово-снабжения; ns(d), nd(d) - инварианты, равные отношению  систолической и диатолической частей ССЦ к их суммарному значению  в пределах физической нагрузки. Кривые I и II соответственно представляют значения ns(d) =0,382Öd и nd(d) =0,618/Öd

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

По аналогии с геометрическими представлениями SR^(п) -система  может быть представлена как "плоскость", поскольку эта система  связана с изменением двух величин - d и W. Эта "плоскость"  обозначена нами как j-"плоскость" полиморфизмов. Ее можно  представить как совокупность полиморфических "линий" некоторого  j-параметра (R^(п)-систем) для множества животных в пределах  вариации нагрузки. Очевидно, что для любого параметра  (длительность, объем, давление, кровоток) можно построить свою  "плоскость" полиморфизмов. В соответствии с (2.13) åR^(п) -системы  отдельных j-параметров изоморфичны друг другу. Изоморфичная система  "плоскостей" полиморфизмов составляет å_Иå_СR^(П) -систему, т.е.  трехмерное "пространство" ССЦ с "координатами": параметр, нагрузка  и вес. Аналогичным образом можно построить "пространство" (2.7)  как полиморфную систему "плоскостей" изоморфизмов (r-"плоскостей",  рис. 2.1). Исходя из вышеизложенного, мы могли убедиться в наличии  в "геометрическом" "пространстве" (2.7) n-мерных объектов:

1)  нульмерного (отдельная ССЦ);

2) одномерного (R -система);

3)  двумерного (j-"плоскость");

4) трехмерного (совокупность  j-"плоскостей" ).

"Пространство" (2.7) может быть представлено как  совокупность либо "точек", либо "линий", либо "плоскостей".  Рассмотрим группу возможных преобразований некоторой "точки"  "пространства" в другие того же "пространства". 

"Пространство" (2.7) состоит из T-, P-, V- и Q-"плоскостей"  полиморфизмов (рис. 2.3); соответственно индексы T, P, V, и Q  указывают на принадлежность " плоскости" к некоторому параметру  (длительность, давление, объем, кровоток). Очевидно, что в  соответствии с (2.10-2.12), (2.13) или (2.14) либо их комбинации  всякая "точка" некоторой "плоскости" полиморфизмов может быть  преобразована в любую другую "точку" на данной "плоскости" или  какой-либо другой. Рассмотрим, например, возможные преобразования  некоторой ССЦ на T-"плоскости" (объект A_Т, рис. 2.3). В первом  варианте по законам (2.10-2.12) имеет место полиморфное  преобразование (A_Т ® A_Т^(П) ).

 

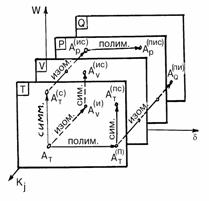
Рис. 2.3. Группа системных пре-образований объектов  "простран-ства" ССЦ. T-, V-, P-, Q- "плос-кости" полиморфизмов; "п", "и", "с", "пи", "пс", "ис", "пис"  - соответственно полиморфное, изо-морфное, симметрийное, полимор-фно-  изоморфное, полиморфно- симметрийное, изоморфно- симмет-рийное,  полиморфно- изоморфно- симметрийное преобразования; A_Т - некоторый  объект T - "плоскости"; A_Т^(П), A_Т^(С), A_V^(И), A_Q^(ПС), A_Т^(ПИ),  A_Р^(ИС), A_Р^(ПИС) - объекты, полу-ченные из объекта A_Т в результате  системных преобразований.  

В данном случае обе ССЦ относятся к  одному и тому же животному при разных уровнях кровоснабжения d. В  другом варианте при фиксированной величине d по закону (2.14)  происходит симметрийное преобразование объекта А одного животного  в аналогичный объект другого животного (A_Т ® A_Т^(С)). В третьем случае  по законам (2.10-2.12) и (2.14) преобразование имеет  полиморфно-симметрийный характер (A_Т ® A_Т^(П) ® A_Т^(С)). В этом случае  объект A_Т в пределах "плоскости" может быть преобразован в объект  аналогичного наименования для другого животного и другого уровня  нагрузки. Естественно, что в пределах данной "плоскости" существует  также и четвертое, тождественное, преобразование объекта в самого  себя (A_Т ® A_Т). Во всех "плоскостях" (T, P, V и Q) в пределах d=1-4  существует симметрия R^(П) -систем относительно одних и тех же  инвариантов n_s(d) и n_d(d) (см. рис. 2.2). Из этого следует  изоморфичность этих "плоскостей" друг другу. Изоморфичное  преобразование объекта A_Т в изоморфичный ему объект другой,  например, Q-"плоскости" происходит по закону (2.13) (A_Т ® A_Т^(И)).  Таким образом, с учетом законов (2.10-2.12), (2.13) и (2.14)  преобразование одного объекта в другой в пределах "пространства"  может иметь либо тождественный, либо полиморфный, либо  симметрийный, либо изоморфный, либо изоморфно-полиморфный, либо  изоморфно- симметрийный, либо изоморфно- полиморфно- симметрийный  характер. Очевидно, что любое комбинированное преобразование одного  объекта в другой можно представить в любой последовательности,  например, либо полиморфно- изоморфное или изоморфно- полиморфное и  либо изоморфно- симметрийное или симметрийно- изоморфное и т.д. Все  эти перестановки на конечный результат преобразования никоим  образом не влияют. Необходимо отметить, что группа установленных  нами преобразований отдельной ССЦ находится в полном соответствии с  первым законом преобразования композиции системы, представленным  Ю.А.Урманцевым [136]. Важно отметить, что преобразования в пределах  "пространства" связаны с использованием величин 0,382, 0,618, a_J,  b_j и k_j, которые обусловливают оптимальный характер преобразований.