Е. В. Бурлаченко
АЛГЕБРАИЧЕСКИЕ ЗАМЕТКИ
(Продолжение; начало см. в [1])
5. Обобщенные
полиномы Чебышева
5.1
Обозначим:
, 
; при 
, 
.
Тогда
,
,
.
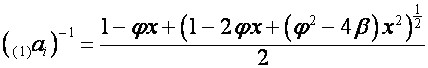Обозначим:
, ; при , 
.
Тогда
,
,
.
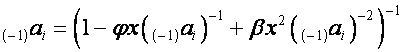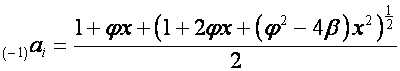Пусть 
, . Составим фрагменты таблиц 
и 
, например, при 
:
.
Для верхней половины таблицы справедливо
равенство 
, 
. Учитывая, что 
, выводим:
,
где 
– полином степени 
(т.е. вектор, все
члены которого, начиная с номера 
, равны нулю), 
.
Матрицу, которая получается из
единичной матрицы размерности 
перестановкой
столбцов в обратном порядке, обозначим 
. Например
;
.
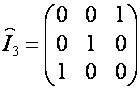По определению преобразования 
-я строка матрицы
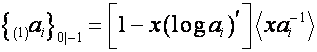
совпадает с -й строкой матрицы 
. Таким образом, полином 
, 
, совпадает с -й строкой матрицы
.
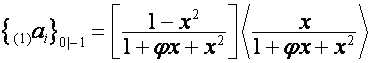Например,
.
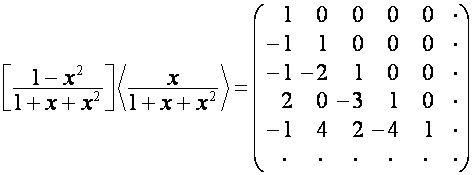Так
как
,
,
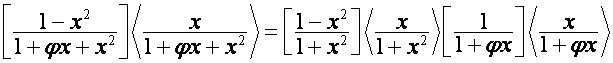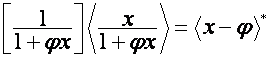то
,
где 
, , – -я строка матрицы
.
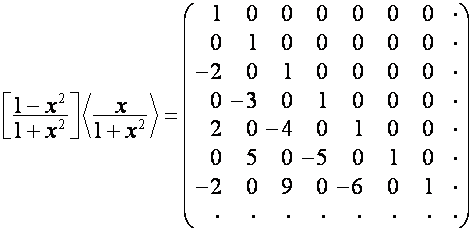Из таблицы
, например,
:
,
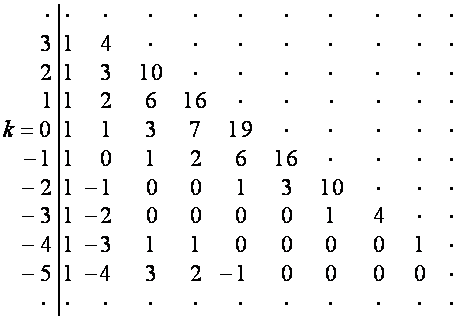где
,
видно,
что
,
или
,
где 
– полином степени 
; 
совпадает с -й строкой матрицы
,
например,
,
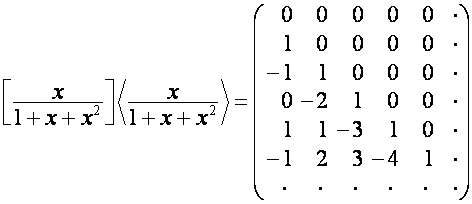так
что
,
где
– -я строка матрицы
.
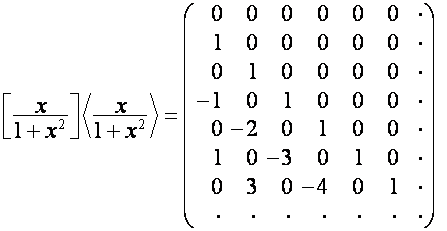Таким образом,
,
;
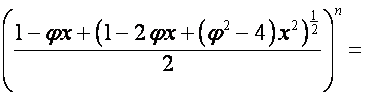
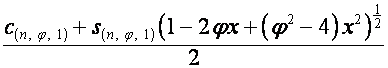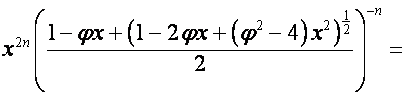
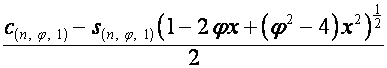Пусть 
, 
. Составим фрагменты таблиц и 
, например, при :
Очевидно, что если 
– полином степени , то
.
Поэтому,
если
,
как
в случае с полиномом 
, то
.
Таким образом, для верхней половины
таблицы справедливо равенство
, .
Следовательно,
,
где 
, 
, , совпадает с -й строкой матрицы
,
,
где 
, , – -я строка матрицы
.
Из таблицы , например,
:
где
,
видно,
что
,
или
,
где
совпадает с -й строкой матрицы
,
,
где 
– -я строка матрицы
.
Таким образом,
,
.
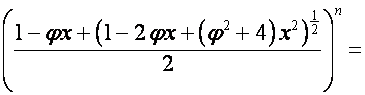
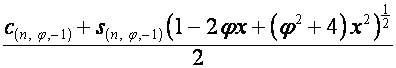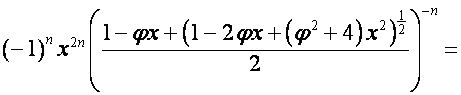
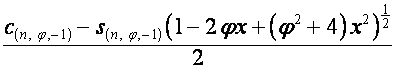Перейдем к общему случаю. Пусть , . Тогда
,
,
,
.
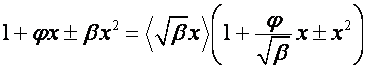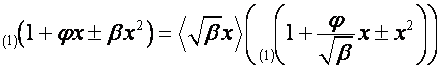Пусть теперь 
, 
– любые действительные
числа. -ю строку матрицы
,
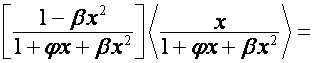
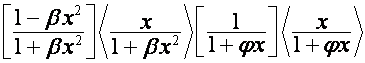, обозначим 
; -ю строку матрицы
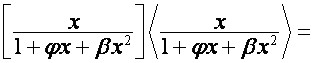
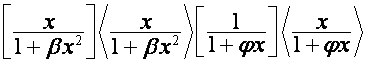
обозначим
. Тогда
,
,
где 
, 
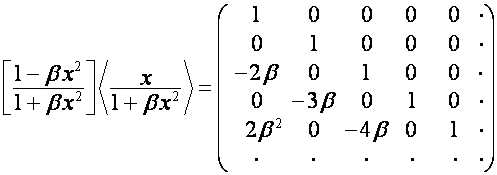– -я строка матрицы
,
– -я строка матрицы
,
,
.
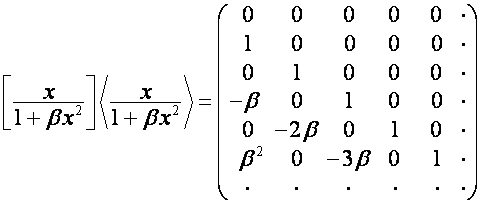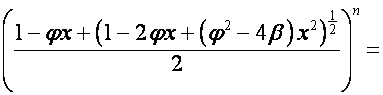
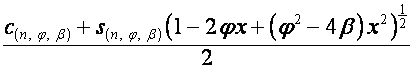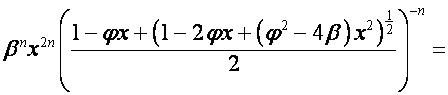
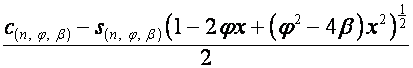Отметим,
что
, 
,
, 
,
, 
.
Отметим также равенство, которое проверяется с помощью
подстановки,
.
5.2
Полиномы Чебышева определяются следующим образом:
,
,
,
;
,
,
,
.
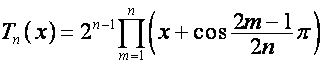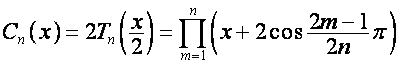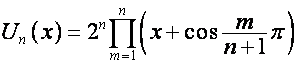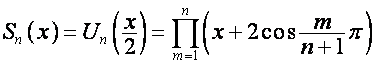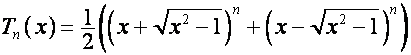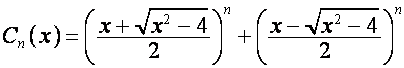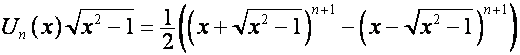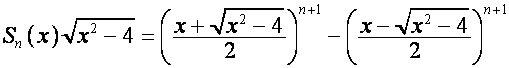Рассмотрим метод, позволяющий выражать
корни некоторых полиномов, к которым относятся и полиномы Чебышева, через корни
полиномов деления круга.
Обозначим:
,
, 
.
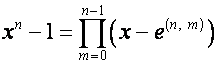Тогда:
,
,
.
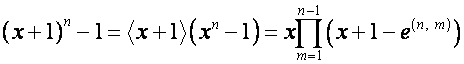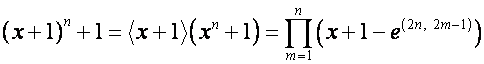Запомним правила преобразования корней
полиномов при следующих элементарных преобразованиях. Если
, 
,
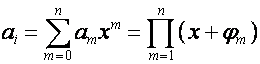то:
,
,
,
.
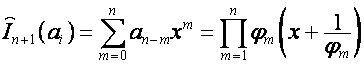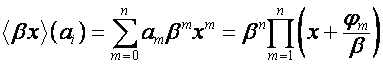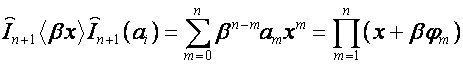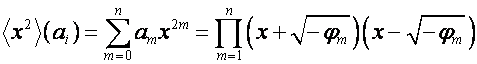Следовательно,
,
,
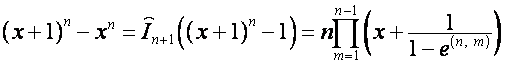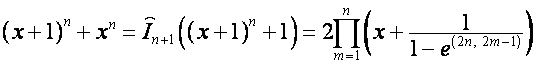где
, 
.
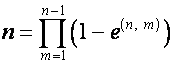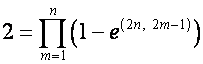Так
как
,
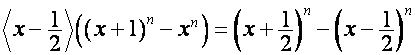то
,
.
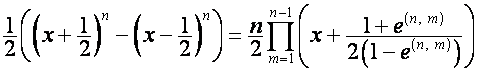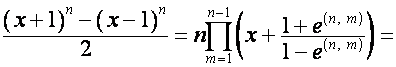
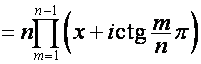Аналогично,
.
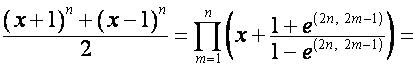
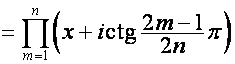Найдем корни полиномов
и 
,
где
.
Обозначим:
.
Так
как
,
то
.
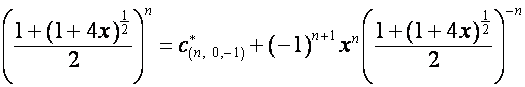Из
таблицы
:
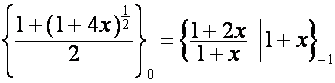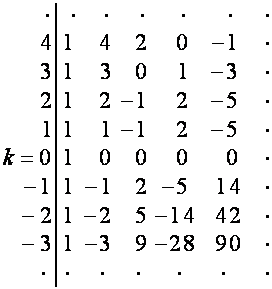
видно,
что 
совпадает с -й строкой матрицы
.
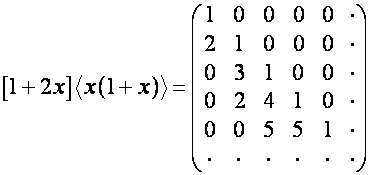Так
как
,
,
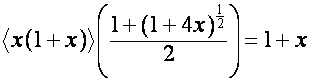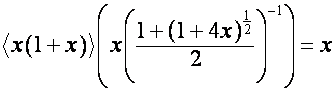то
,
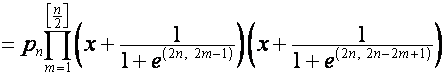где 
– целая часть от 
, 
, 
. Степень полинома 
обусловлена тем, что 
, если нечетно и 
. Обозначим:
.
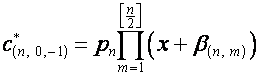Тогда
,
,
.
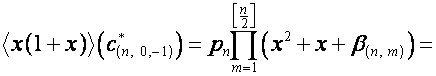
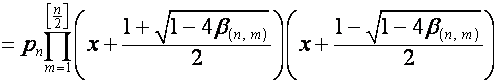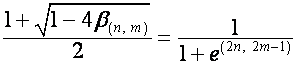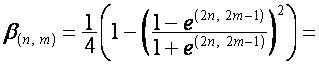
Таким образом,
,
,
,
.
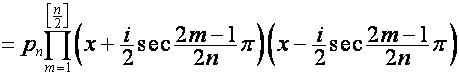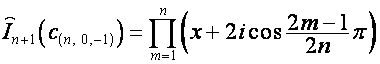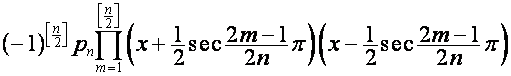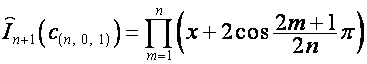Найдем корни полиномов
и 
.
Обозначим:
.
Из
таблицы
:
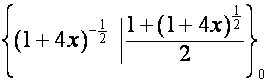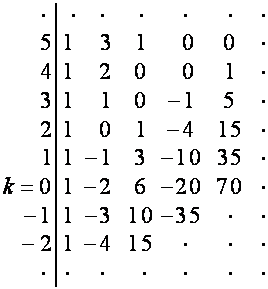
видно,
что
,
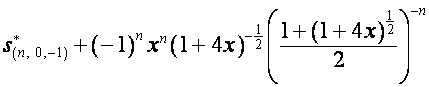где 
совпадает с -й строкой матрицы
.
Так
как
,
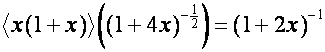то
,
где
, 
, 
.
Степень 
обусловлена тем, что 
, если четно и 
. Обозначим:
.
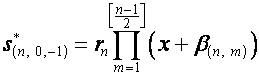Тогда
,
.
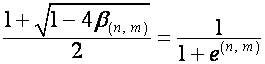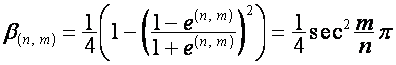Таким образом,
,
,
,
.
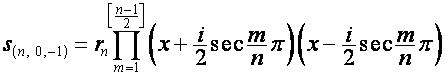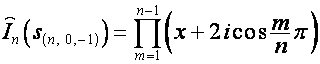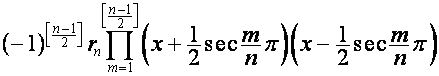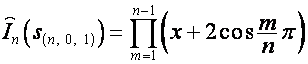В общем случае:
,
,
,
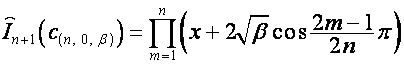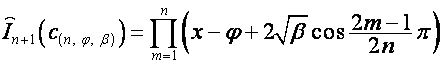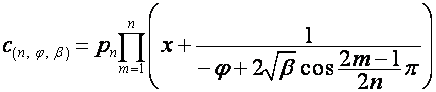где
.
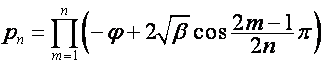Если один из сомножителей множителя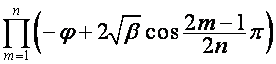 
равен нулю , он вместе
с соответствующим ему полиномом
заменяется на 
.
Аналогично,
,
,
,
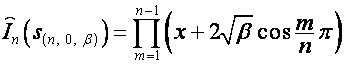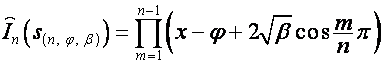где
.
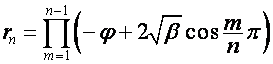5.3
Обозначим:
, ; при , .
Тогда
,
,
.
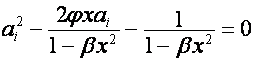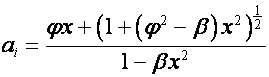Обозначим:
, ; при , .
Тогда
,
,
.
Раскладывая 
в бином Ньютона и
группируя члены, можно представить его в виде
,
где 
– полином степени , четные члены которого равны нулю, если нечетно, нечетные
члены равны нулю, если четно; 
– полином степени , четные члены которого равны нулю, если четно, нечетные члены
равны нулю, если нечетно. Например:
, 
;
, 
,
, 
,
, 
,
, 
.
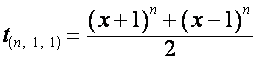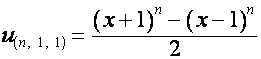Так как
,
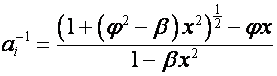то
,
,
,
.
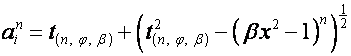-й член 
-й восходящей диагонали таблицы , т.е. -й член вектора
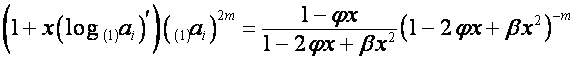
равен -му члену полинома 
. Отсюда вытекает, что 
совпадает с -й строкой матрицы
.
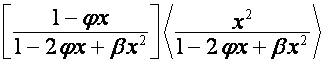Например:
:
;
:
;
:
;
:
.
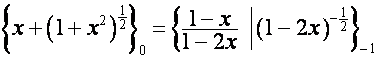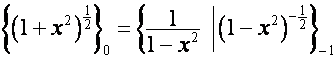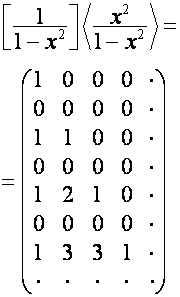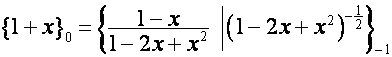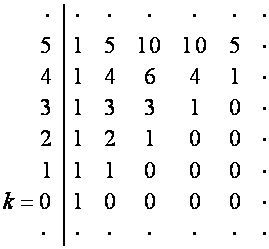
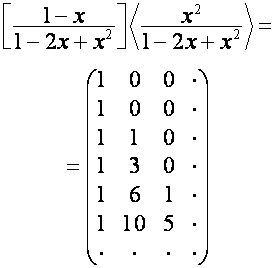Обозначим:
.
Так
как
,
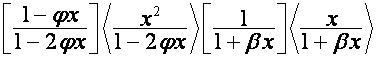то
.
Так
как
,
то
.
Так
как
,
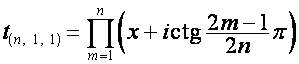то
, 
, 
,
,
,
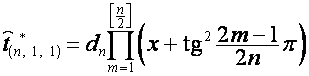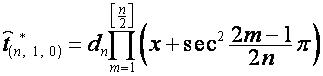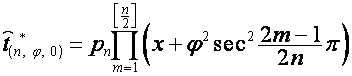где
, 
,
,
,
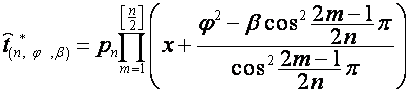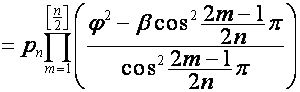
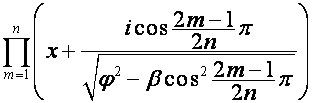где множитель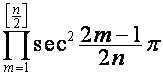 
равен 
, если четно, и 
, если нечетно (проверяется
подстановкой 
, ); если один из сомножителей (в случае 
– любой из
сомножителей) множителя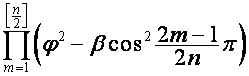 
равен нулю, он
заменяется на 
, соответствующая ему пара полиномов заменятся на . Отметим также, что 
.
-й член вектора 
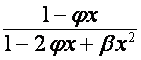равен -му члену полинома и нулю, если степень меньше . Следовательно,
,
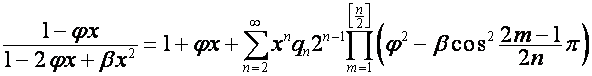где 
, 
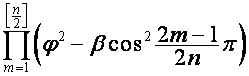, множитель равен нулю, если один
из сомножителей равен нулю.
Обозначим:
, 
.
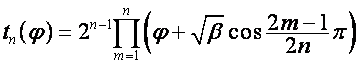Тогда
.
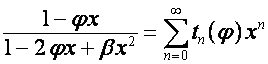Так
как
,
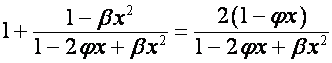то
.
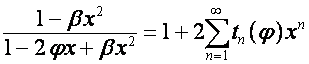Убедимся, что
.
Следовательно,
-я строка верхней половины таблицы
имеет
вид
.
-й член -й восходящей диагонали таблицы 
, 
, т.е. -й член вектора 
, равен -му члену полинома 
. Отсюда вытекает, что 
совпадает с -й строкой матрицы
.
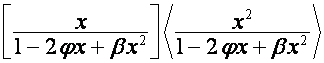Например:
:
;
:
;
:
;
:
;
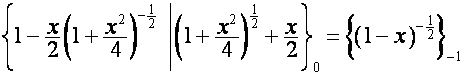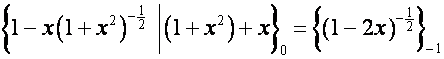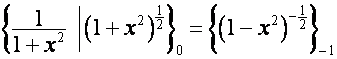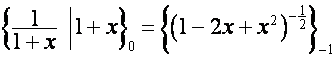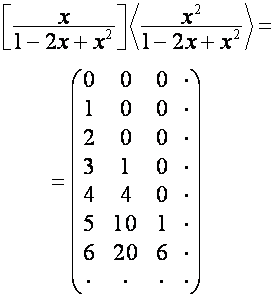Обозначим:
.
Так
как
,
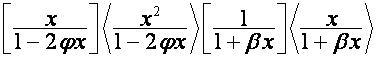то
.
Так
как
,
то
.
Так
как
, 
, 
,
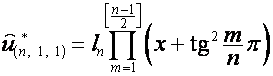то
,
,
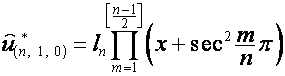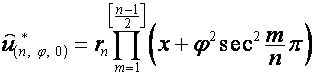где
, ,
,
,
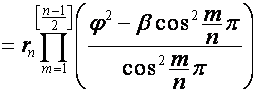
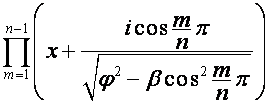где множитель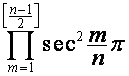 
равен , если четно, и , если нечетно; если один из
сомножителей (в случае 
– любой из
сомножителей) множителя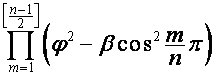 
равен нулю, он
заменяется на 
, соответствующая ему пара полиномов заменяется на . Отметим, что 
.
-й член вектора 
равен -му члену полинома 
и нулю, если степень меньше . Следовательно,
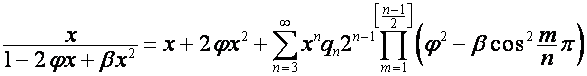
где 
, 
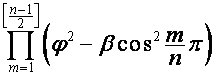, множитель равен нулю, если один
из сомножителей равен нулю.
Обозначим:
, 
, 
.
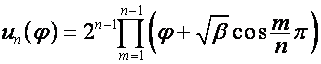Тогда
.
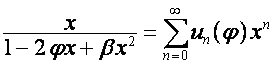Отметим равенства, словно предназначенные
для обеспечения преобразований полиномов данного вида. Подставляя в общие
формулы полиномов 
, 
значения , , получаем:
, 
,
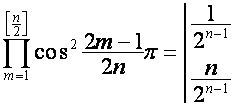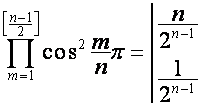где верхнее значение берется при четном , нижнее – при нечетном . Подставляя в общие формулы полиномов значения , 
, получаем:
, 
.
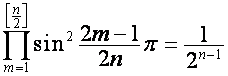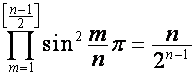1.
Е. В. Бурлаченко. Алгебраические заметки.